Introduction
Position du problème :
Considérons un système différentiel de la forme \(X' = A X\), où \(A\) est une matrice réelle constante à deux lignes et deux colonnes.
Si l'on pose \(\displaystyle{A=\left(\begin{array}{cc}a & b \\ c & d\end{array}\right)}\) le système s'écrit
\(\displaystyle{\left\{\begin{array}{ll}x'=ax+by \\ y'=cx+dy \end{array}\right.}\)
Nous avons appris dans le chapitre précédent à résoudre un tel système : la forme des solutions dépend du type des valeurs propres de la matrice \(A\).
Chaque solution \((x(t), y(t))\) est l'équation paramétrique d'une courbe du plan \((x, y)\). Cette courbe est la trajectoire[1] de la solution.
Nous savons que par chaque point du plan \((x, y)\) passe une de ces courbes et une seule. En d'autres termes, deux trajectoires distinctes ne se rencontrent pas ; rappelons cependant qu'en général une même trajectoire est parcourue, à des instants différents, par une infinité de solutions. Rappelons aussi que l'ensemble des trajectoires d'un système donné se nomme le portrait de phase du système
Le point \((0,0)\) est toujours un point stationnaire[2] (ou point critique, ou point d'équilibre du système). C'est la trajectoire de la solution nulle \((x(t) = 0, y(t) = 0)\).
Si la matrice \(A\) est inversible (c'est à dire si \(0\) n'est pas une valeur propre de \(A\)), c'est même le seul point stationnaire. Les autres trajectoires sont des courbes qui ne passent pas par l'origine.
Exemple de portrait de phase
Considérons le système
\(x' = y\)
\(y' = -x\)
Ses solutions s'écrivent \(\displaystyle{\left\{\begin{array}{ll}x(t)=A\cos t+B\sin t \\ y(t)=-B\cos t+A\sin t \end{array}\right.}\)
Les trajectoires des solutions non nulles sont les cercles centrés à l'origine, de rayon \(\sqrt{A^2+B^2}\).
Il suffit d'en dessiner quelques uns pour imaginer les autres
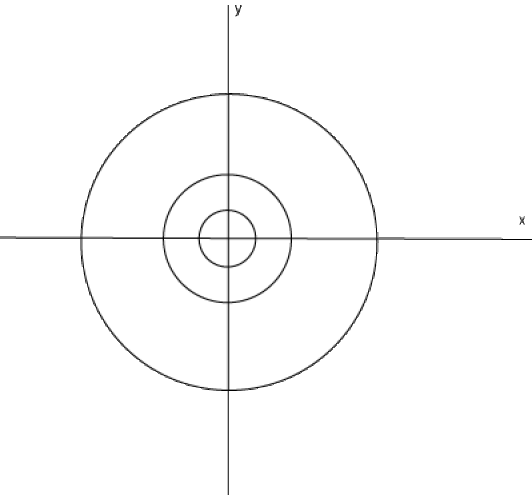
Remarquons que deux solutions distinctes
\(\displaystyle{\left\{\begin{array}{ll}x(t)=A\cos t+B\sin t \\ y(t)=-B\cos t+A\sin t \end{array}\right.}\)
et
\(\displaystyle{\left\{\begin{array}{ll}x_1(t)=C\cos t+D\sin t \\ y_1(t)=-D\cos t+C\sin t \end{array}\right.}\)
telles que \(A^2+B^2 = C^2 + D^2\) ont la même trajectoire.
Nous allons étudier, selon une classification due à Henri Poincaré, le type des portraits de phase d'un système linéaire en fonction du type de valeurs propres de la matrice A.