Résistance équivalente à un réseau
Durée : 2 mn
Note maximale : 4
Question
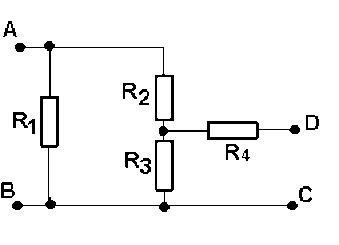
Toutes les résistances ont pour valeur \(1 \mathrm{ k} \Omega\).
Par quelle résistance unique peut-on remplacer le circuit :
vu entre les points \(A\) et \(B\) ?
vu entre les points \(C\) et \(D\) ?
Solution
\(R_{\textrm{\'eq} AB} = R_1 // ( R_2 + R_3 )\)
\(\displaystyle{ \frac{1}{R_{\textrm{\'eq} AB}} = \frac{1}{R_1} + \frac{1}{R_2 + R_3} }\)
\(\displaystyle{ R_{\textrm{\'eq} AB} = \frac{R_1(R_2+R_3)}{R_1 + R_2 + R_3} = \frac{2}{3} = \mathrm{0,66 k} \Omega}\) (2 pts)
\(R_{\textrm{\'eq} AB} = R_4 + R_3 // ( R_1 + R_2 )\)
\(\displaystyle{ R_{\textrm{\'eq} AB} = R_4 + \frac{R_3(R_1+R_2)}{R_1 + R_2 + R_3} = 1 + \frac{2}{3} = \mathrm{1,66 k} \Omega}\) (2 pts)