Théorème de Gauss

En traçant deux réseaux de lignes sur une surface quelconque, \(S\), on la décompose en surfaces plus petites, délimitées par ces lignes (voir la figure).

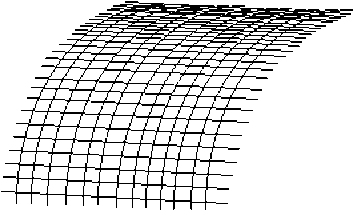
Si les lignes sont très nombreuses et si elles sont distribuées régulièrement, chacune de ces surfaces a une aire très petite. Soit un point, \(M\), de la surface (\(S\)). Si le nombre des lignes augmente indéfiniment, la petite surface où se trouve le point, \(M\), diminue et tend à se rapprocher de la portion de plan tangent en \(M\), à la surface (\(S\)). A la limite, son aire, \(\mathrm dS\), est infiniment petite et elle se confond avec une portion de plan. On l'appelle élément de surface entourant le point, \(M\). On peut ainsi considérer qu'une surface quelconque, \(S\), est la juxtaposition d'un nombre infini d'éléments de surface \(\mathrm dS\).