Relation entre flux et angle solide
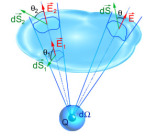
Soit un point \(M\) appartenant à l'élément de surface \(dS\). Le champ \(\vec E\) créé en \(M\) par la charge \(Q\) est porté par \(OM\) et dirigé de \(O\) vers \(M\) si \(Q > 0\) ; son module est
\(|\vec E| = \frac{Q}{4 \pi \epsilon_0 r^2}\) avec \(r = OM\).
Le flux élémentaire de ce champ électrique à travers l'élément de surface \(dS\) entourant le point \(M\) est :
\(\mathrm d \Phi = |\vec E| \mathrm d S \cos~\theta\) ; \(~\mathrm d \Phi = \frac{1}{4 \pi \epsilon_0} ~ \frac{Q}{r^2} ~ \mathrm d S \cos~\theta\)
Or \(\frac{\mathrm d S \cos~\theta}{r^2}\) est l'angle solide \(\mathrm d \Omega\) sous lequel le contour de \(dS\) est vu de \(O\) (géométriquement, c'est un cône de sommet \(O\) qui est tangent à l'élément de surface \(dS\)).
\(\mathrm d \Phi = \frac{Q}{4 \pi \epsilon_0 r^2} ~ \mathrm d S \cos~\theta = \frac{Q}{4 \pi \epsilon_0} ~ \mathrm d \Omega\)