Notion de flux
Désignons par \(\vec E\) le vecteur champ électrique au point \(M\). Soit \(\mathrm dS\) l'élément de surface entourant ce point et le vecteur \(\mathrm d \vec S\) correspondant.
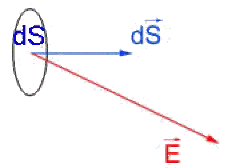
Définition :
Par définition, le flux \(\mathrm d \Phi\) du champ électrique \(\vec E\) à travers l'élément de surface considéré \(\mathrm d S\) est égal au produit scalaire
\(\mathrm d \Phi = \vec E . \mathrm d \vec S\)
On l'appelle flux élémentaire pour indiquer qu'il est relatif à un élément de surface.
Le signe du flux dépend du sens du vecteur \(\mathrm d \vec S\). Considérons en effet les deux vecteurs opposés, \(\mathrm d \vec S\) et \(\mathrm d \vec S'\), associés à un élément de surface.
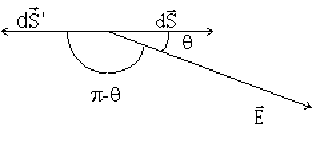
Si le vecteur \(\mathrm d \vec S\) fait avec le champ électrique \(\vec E\) l'angle \(\theta\), le vecteur \(\overrightarrow{\mathrm dS'}\) fait l'angle \(\pi-\theta\), et comme \(\cos ~ (\pi - \theta) = - \cos~\theta\), les produits scalaires \(\vec E . \mathrm d \vec S\) et \(\mathrm d \vec S'\) ont des valeurs opposées.
Pour calculer le flux algébrique du champ électrique \(\vec E\) à travers un élément de surface \(\mathrm d \vec S\), il faut donc choisir, en accord avec la notion de flux positif, le sens du vecteur \(\mathrm d \vec S\) associé à cet élément.