Théorème de Gauss

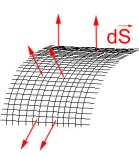
On associe à cet élément un vecteur appelé vecteur "normale" \(\mathrm d \vec S\) défini de la manière suivante : son origine est un point \(M\) de l'élément ; sa direction est normale à la surface ; son module est égal à l'aire \(\mathrm dS\). Le vecteur \(\mathrm d \vec S\) est donc infiniment petit. Son orientation est choisie arbitrairement (vers l'extérieur pour les surfaces fermées). Pour orienter \(\mathrm d \vec S\), on peut aussi utiliser la règle du "tire-bouchon" . On oriente le contour \(C\) délimitant la surface en choisissant arbitrairement un sens de parcours positif (\(+\)). Le vecteur \(\mathrm d \vec S\) est orienté suivant la progression d'un tire-bouchon tournant dans le sens (\(+\))