Circulation d'une force radiale
Durée : 3 mn
Note maximale : 11
Question
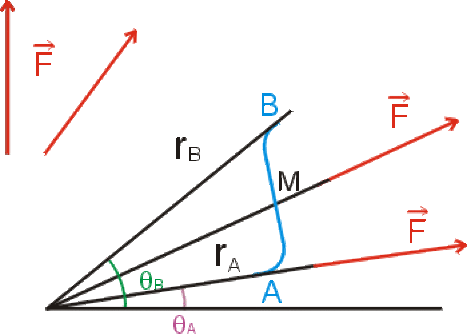
Soit un champ de forces radiales \(||\vec F||=\textrm{cte}=5N\) dans un plan.
Calculer la circulation de \(\vec F\) sur un trajet \(AB\) quelconque : \(r_A = 1 m~r_B = 3 m~\theta_A=\frac\pi6~\theta_B=\frac\pi3\)
Solution
En rapportant le plan à deux vecteurs de base orthonormés \(\vec u_r\) radial et \(\vec u_{\theta}\) orthoradial, un déplacement \(d\vec M\) élémentaire s'écrit : \(d\vec M=dr.\vec u_r+rd\theta.\vec U_\theta\) et \(\vec F=F\) \(\vec u_r.\vec u_\theta=0\)
\(C_{A\rightarrow B}=\displaystyle{\int_{AB}\vec F.d\vec M=\int_{AB}F.\vec u_r.(dr.\vec u_r+rd\theta.\vec u_\theta)=\int_{r_A}^{r_\theta}F.dr}\)
\(C_{A\rightarrow B}=F(r_B-r_A)\) car \(\vec u_r.\vec u_r=1\) et \(\vec u_r.\vec u_\theta=0\)
\(C_{A\rightarrow B}=10\textrm{ J}\)
Evaluation :
Ecriture de \(d\vec M\) : 4 pts
Ecriture \(C_{A\rightarrow B}\) : 3 pts
Calcul de \(C_{A\rightarrow B}\) : 4 pts