Circulation d'une force sur un contour fermé
Durée : 5 mn
Note maximale : 10
Question
Soit un champ de forces non uniformes.
\(y_3=3m\quad||\vec F||=F_3=3N\quad y_1=1m\quad||\vec F||=F_1=5N\quad y_2=3m\quad||\vec F||=F_2=3N\forall x\)
Calculer la circulation de \(\vec F\) sur un rectangle \(ABCD\) : \(x_B = 4 m ; x_A = 1m\)
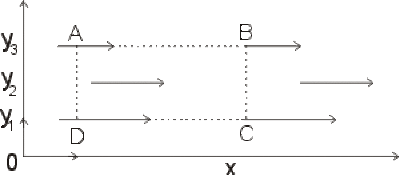
Solution
\(C_{ABCDA}=\displaystyle{\int_{AB}\vec F.d\vec M+\int_{BC}\vec F.d\vec M+\int_{CD}\vec F.d\vec M+\int_{DA}\vec F.d\vec M}\)
\(\displaystyle{\int_{BC}\vec F.d\vec M}\) et \(\displaystyle{\int_{DA}\vec F.d\vec M}=0\) car \(\vec F\) est orthogonal à \(d\vec M\) (3 pts)
Pour les 2 autres trajets : \(\vec F=F.\vec u_x\) et \(d\vec M=dx.\vec u_x\)
\(\int_{AB}\vec F.d\vec M=\int_{AB}F\vec u_x.dx.\vec u_x=\int_{X_A}^{X_B}Fdx=F_3(X_B-X_A)=3\times3=9 \textrm J\) (3 pts)
\(\displaystyle{\int_{CD}\vec F.d\vec M=F1(X_0-X_C)=5\times(-3)=-15~J}\) (3 pts)
\(C_{ABCDA}=9-15=-6~J\) (1 pt)