Courant volumique - Intensité d'un courant [Le champ magnétostatique]

Courant volumique - Intensité d'un courant

On appelle courant électrique tout mouvement d'ensemble de charges par rapport à un référentiel donné \(\mathcal{R}\).
En un point \(M\) de ce courant composé de particules de charge \(q\), on désigne par :
\(n(M,t)\) leur nombre par unité de volume,
\(\vec v(M,t)\) leur vitesse d'ensemble par rapport à \(\mathcal{R}\)
On distingue trois types de courants :
Les courants particulaires ou courants dans le vide. Ce sont par exemple les faisceaux d'électrons, d'ions.
Les courants de conduction qui correspondent à des déplacements de charges dans un support conducteur comme un métal ou un électrolyte.
Les courants de convection créés par le déplacement d'un conducteur ou d'un isolant chargé.

Soit un élément de surface^[1] \(\overrightarrow{\mathrm d\mathfrak{S}}\) centré autour d'un point \(\mathsf M\).
La charge mobile \(\mathrm d q_m\) qui traverse \(\overrightarrow{\mathrm d\mathfrak{S}}\) entre les dates \(t\) et \(t + \mathrm {d}t\) est contenue dans le cylindre de base \({\mathrm d\mathfrak{S}}\) et de génératrices \(\vec{v} \mathrm {d}t\) .
Elle a pour expression : \(\mathrm {d}q_m = n. q \vec v \mathrm {d} t .\overrightarrow{\mathrm d\mathfrak{S}}\)

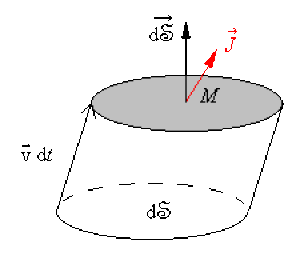
Le vecteur \(\vec{J}(M, t) = nq \vec v\) est appelé courant volumique ou densité volumique de courant. En posant \(nq = \rho_m\) densité de charge mobile, le vecteur courant volumique peut également s'écrire : \(\vec{J}(M,t) = \rho_m \vec v\)

L'intensité du courant qui traverse l'élément de surface \(\overrightarrow{\mathrm d\mathfrak{S}}\) s'écrit : \(\mathrm{d}I=\frac{\mathrm{d}q_m}{\mathrm dt}=\vec J.\overrightarrow{\mathrm d\mathfrak{S}}\).
Compte tenu de la définition de \(\vec J\), l'intensité d'un courant est la quantité d'électricité qui traverse l'élément de surface \(\mathrm d\mathfrak{S}\) pendant l'unité de temps.
Si \(\mathrm{d}\mathcal{Q}_m\), désigne la quantité totale d'électricité qui traverse une surface \(\mathfrak S\) pendant l'intervalle de temps \(\mathrm{d}t\), l'intensité du courant correspondante est : \(I = \iint_\mathfrak{S} \vec J .\overrightarrow{ \mathrm{d}\mathfrak{S}} = \frac {\mathrm {d}\mathcal{Q}_m} {\mathrm {d}t}\)
Le sens du courant est donné par \(\vec J\). Si \(q < 0\), \(\vec J\) est de sens opposé à celui du déplacement des charges, ce qui correspond au cas de la conduction dans un conducteur.

Elément de surface
Considérons un élément de surface d'aire dS.
On associe à cet élément un vecteur appelé vecteur "normale" \(\overrightarrow{\mathrm{d}\mathrm S}\) défini de la manière suivante : son origine est un point M de l'élément ; sa direction est normale à la surface ; son module est égal à \(\mathrm {dS}\) . Le vecteur \(\overrightarrow{\mathrm {d}\mathrm S}\) est donc infiniment petit. Son orientation est choisie arbitrairement (vers l'extérieur pour les surfaces fermées). Pour orienter \(\overrightarrow{\mathrm {d}\mathrm S}\) , on peut aussi utiliser la règle du "tire-bouchon" . On oriente le contour C délimitant la surface en choisissant arbitrairement un sens de parcours positif \((+)\) Le vecteur \(\overrightarrow{\mathrm {d}\mathrm S}\) est orienté suivant la progression d'un tire-bouchon tournant dans le sens \((+)\)