Eléments de courants
En électrostatique on introduit la notion d'éléments de charge \({\mathrm{d}q}\) ; nous allons définir ici les éléments de courant \(\overrightarrow{\mathrm dC}\).
Considérons un parallélépipède rectangle élémentaire de dimensions \(\mathrm{d}x\), \(\mathrm{d}y\), \(\mathrm{d}l\) traversé par un courant volumique \(\vec J\) parallèle à \(\overrightarrow{\mathrm dl}\)
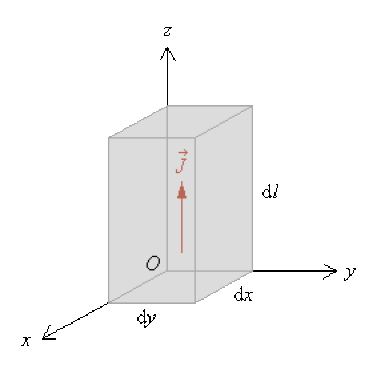
Ce parallélépipède constitue un élément de courant \(\overrightarrow{\mathrm dC}\) tel que :
\(\overrightarrow{\mathrm dC} = \vec J . \mathrm{d}\mathfrak{V} = \rho_m~\vec v~\mathrm{ d}x~\mathrm{ d}y~\mathrm{ d}l\)
Si \(\mathrm{d}x\) tend vers zéro, \(\vec J\) n'est plus volumique mais surfacique. \(\rho_m~\mathrm{d}x\) tend vers \(\sigma_m\) et, en posant \(\mathrm{d}\mathfrak{S}_S = \mathrm{d}y \mathrm{ d}l\) , on a alors :
\(\overrightarrow{\mathrm dC} = \sigma_m \vec v \mathrm{ d}y \mathrm{ d}l = \vec J_S . \mathrm{d}\mathfrak{S}_S\), avec \(\vec J_S = \sigma_m \vec v\)
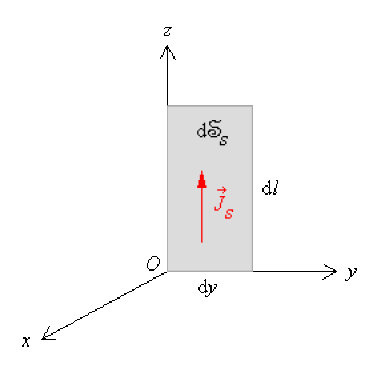
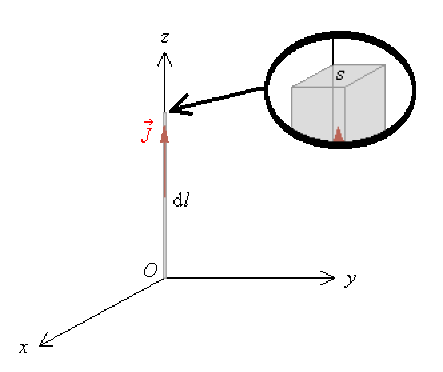
Si le conducteur est de très faible section \(s\), alors
\(\overrightarrow{\mathrm d C} = \rho_m ~ \vec v ~ s \mathrm{ d}l = \vec J ~ s . \mathrm{d}l = \vec J s \mathrm{ }\vec e_z . \mathrm{d}l \mathrm{ }\vec e_z = l \mathrm{ }\overrightarrow {\mathrm d l}\)
Comparaison des expressions des éléments de charges et des éléments de courants
Remarque :
il ne faut surtout pas confondre l'élément de courant \(\overrightarrow {\mathrm d C}\) et l'intensité élémentaire \(\mathrm d l\).
En effet :
pour un courant volumique :
\(\mathrm d l= \vec J . \vec{\mathrm d \mathfrak{S}} = \rho_m v \mathrm{ d} x \mathrm{ d}y = J \mathrm{ d} x \mathrm{ d}y = J \mathrm{d}\mathfrak{S}_n\)
\(\mathrm{d}\mathfrak{S}_n\) étant l'aire de l'élément de surface orthogonal à \(\vec J\).
pour un courant surfacique :
\(\mathrm{d} I = \sigma_m v \mathrm{d}y = J_s \mathrm{d}y = J_s \mathrm{d}l_n\)
\(\mathrm{d}l_n\) étant la longueur de la "section" orthogonale à \(\vec J\).