Le champ magnétostatique

• La rupture de l'équilibre des charges qui donne naissance à un courant électrique dans un milieu conducteur peut avoir diverses origines.

  Si le courant est dû uniquement à l'existence d'un champ électrique \(\vec E(M,t)\), pour un grand nombre de milieux conducteurs et dans un assez grand domaine de validité :

  \(\vec J(M,t) = \gamma(M) \vec E(M,t)\)

  Cette relation, dans laquelle \(\gamma(M)\) est la conductivité électrique du milieu conducteur, constitue la loi d'Ohm locale.

  La conductivité électrique s'exprime en siemens par mètre \((\mathrm{S.m}^{-1})\).

  Dans le cas d'un régime stationnaire, les grandeurs étant indépendantes du temps, elle s'écrit :

  \(\vec J(M) = \gamma(M) \vec E(M)\)

• Compte tenu de la forme locale de la loi d'Ohm, la relation locale de conservation de la charge en régime stationnaire s'écrit :

  \(\mathrm{div} \vec J(M) = \mathrm{div}\mathrm [\gamma(M) \vec E(M)] = 0\)

  Pour un conducteur homogène \(\gamma(M) = \gamma\) alors \(\mathrm{div} \vec E(M) = 0\)

  Par identification avec l'équation de Poisson de l'électrostatique \(\mathrm{div} \vec E(M) = \frac{\rho(M)}{\epsilon_0}\) , on obtient \(\rho(M) = 0\), ce qui signifie qu'il y a bien autant d'électrons qui entrent que d'électrons qui sortent à travers une surface fermée.

  Attention de ne pas confondre \(\rho(M)\) et \(\rho_m\). En effet, \(\rho(M) = 0\) mais \(\rho_m \neq 0\) puisqu'il y a déplacement de charges.

Considérons le cas particulier d'un conducteur cylindrique, de longueur \(\mathit{l}\) , de conductivité \(\gamma\), de section droite constante \(\mathfrak{S}\), traversé par un courant continu d'intensité \(\mathit{l}\).

Comme \(I = \mathrm{Cte}\) , \(J = \mathrm{Cte}\) et \(E = \mathrm{Cte}\), la différence de potentiel entre les extrémités du conducteur a pour expression : \(\displaystyle{V_1 - V_2 = \int_0^l \vec E . \vec{\mathrm{d}l} = El}\)

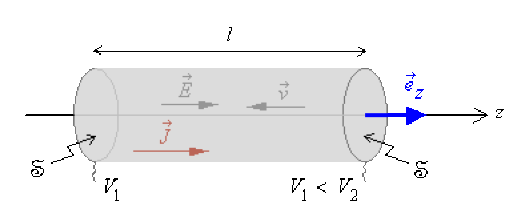
L'intensité du courant qui circule dans ce conducteur a pour expression :

\(I = \iint_\mathfrak{S} \vec J .\overrightarrow{\mathrm{d}\mathfrak{S}} = \iint_\mathfrak{S} \gamma ~E ~\vec e_z . \vec e_z~\mathrm{d}\mathfrak{S}= \iint_\mathfrak{S}~ \gamma~ E~ \mathrm{d}\mathfrak{S} = \gamma~ E~\mathfrak{S} = \frac {\gamma~ \mathfrak{S}}{l}(V_1 - V_2)\)

Cette forme intégrale de la loi d'Ohm donne : \(V_1 - V_2 = RI\)

en posant \(R = \frac l{\gamma ~ \mathfrak{S}}\), résistance du conducteur de section \(\mathfrak{S}\) constante, de longueur \(l\) , parcouru par un courant tel que \(\vec J\) soit parallèle à ses génératrices.

La résistance s'exprime en ohm \((\Omega)\).