Equation de conservation de la charge [Le champ magnétostatique]

Equation de conservation de la charge

Cas général

Soit un volume \(\mathfrak{V}\) délimité par une surface fermée \(\circledS\).

La charge totale \(Q(t)\) à l'intérieur de \(\circledS\) varie dans le temps et on suppose que cette variation ne peut être attribuée qu'à des échanges de charges avec l'extérieur, c'est-à-dire qu'il n'y a aucun centre de production ou de disparition de charges en différents points de \(\mathcal{V}\).

Soit \(\rho (M,t)\) la densité volumique de charge à l'intérieur de \(\mathfrak{ S}\).

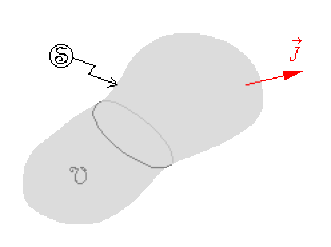
En raison du principe de conservation de la charge, comme il n'y a ni production ni disparition de charges dans \(\mathfrak{V}\) durant un intervalle de temps \(\mathrm d t\) , la variation \(\mathrm d \mathfrak Q\) de la charge \( \mathfrak Q( t)\) intérieure à \(\circledS \)est telle que : \(\mathrm d \mathfrak Q = - \mathrm d \mathfrak Q_m\)

\(\mathrm d\mathfrak Q_m\) désignant la charge mobile qui à traversé la surface \(\circledS\) pendant cette durée \(\mathrm d t\).

Comme \(I = \frac {\mathrm d \mathfrak Q_m} {\mathrm d t} = \oiint_\mathfrak S \vec J . \overrightarrow{\mathrm d \mathfrak S}\), on a \(I = -\frac {\mathrm d \mathfrak Q}{\mathrm d t} = \oiint_\mathfrak S \vec J . \overrightarrow{\mathrm d \mathfrak S}\).

La charge contenue à l'intérieur de \(\mathfrak S\) étant égale à \(\mathfrak Q(t) = \iiint_{\mathfrak{V}} \rho (M,t)\mathrm d \mathfrak{V}\),

on obtient :

\(\frac{\mathrm d \mathfrak Q}{\mathrm d t} =\frac{\mathrm d}{\mathrm d t} \iiint_{\mathfrak{V}} \rho (M,t)\mathrm d \mathfrak{V}= \iiint_{\mathfrak{V}} \frac {\partial \rho (M,t)}{\partial t}\mathrm d\mathfrak{V} = - I = - \oiint_\mathfrak{S} \vec J . \overrightarrow {\mathrm d \mathfrak{S}}\)

La relation \(\oiint_\mathfrak{S} \vec J . \overrightarrow {\mathrm d \mathfrak{S}} = - \iiint_\mathfrak{V} \frac {\partial \rho (M,t)}{\partial t} \mathrm d\mathfrak{V}\) est la forme intégrale de l'équation de conservation de la charge.

Avec le théorème de la divergence^[1] on a :

\(\oiint_\mathfrak{S} \vec J .\overrightarrow {\mathrm{d}\mathfrak{S}} = \iiint_\mathfrak{V}\mathrm{div} \vec J \mathrm{d}\mathfrak{V} = - \iiint_\mathfrak{V} \frac{ \partial \rho }{\partial t}\mathrm{d}\mathfrak{V}\)

La relation \(\mathrm{div} \vec J(M,t) = - \frac{ \partial\rho(M,t) }{\partial t}\) est la forme locale de l'équation de conservation de la charge.

Cas des régimes stationnaires

Toutes les grandeurs sont alors indépendantes du temps et les équations de conservation de la charge s'écrivent : \(\oiint_\mathcal{S} \vec J . \overrightarrow{\mathrm{d} \mathcal{S}} = 0\) et \(\mathrm{div}\vec J(M) = 0\)

Complément : Phénomène stationnaire

Un phénomène stationnaire est caractérisé par des grandeurs indépendantes du temps.

Conséquences

Considérons une surface fermée \(\circledS\) constituée par une portion de conducteur limitée par les sections \(\mathfrak{S}_1\) et \(\mathfrak{S}_2\)

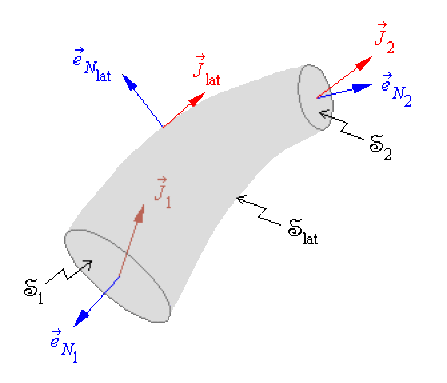
Puisque les charges ne peuvent sortir, le vecteur \(\vec J\) est tangent à la surface latérale \(\mathfrak{S}_\mathrm{lat}\) du conducteur.

La conservation de la charge s'écrit :

\(\oiint_\mathfrak{S}\vec{J}.\vec{\mathrm{d}\mathfrak{S}}=0=\iint_{\mathfrak{S}_1}\vec{J_1}.\vec{\mathrm{d}\mathfrak{S}}_1+\iint_{\mathfrak{S}_2}\vec{J_2}. \vec{\mathrm{d}\mathfrak{S}_2}+\iint_{\mathfrak{S}_{\mathrm{lat}}}\vec{J_\mathrm{lat}}.\overrightarrow{\mathrm{d}\mathfrak{S}_\mathrm{lat}}\).

Le flux à travers la surface latérale étant nul puisque \(\vec J_\mathrm{lat}\) et \(\vec{\mathrm{d}\mathfrak{S}_\mathrm{lat}}\) sont orthogonaux, il vient :

\(\oiint_\mathfrak{S} \vec J . \vec{\mathrm{d}\mathfrak{S}} = \iint_{\mathfrak{S}_1}\vec J_1 .\overrightarrow{\mathrm{d}\mathfrak{S}_1} + \iint_{\mathfrak{S}_2}\vec J_2 . \overrightarrow{\mathrm{d}\mathfrak{S}}_2 = -I_1 + I_2 = 0\),

soit \(I_1 = I_2 = I\) : l'intensité est la même dans toutes les sections d'un conducteur en régime stationnaire c'est-à-dire en courant continu.

La relation précédente montre que, dans un conducteur de section constante, J garde toujours la même valeur.

Notes

Divergence
- On appelle divergence au point M du champ vectoriel \(\vec B (M) \) , le scalaire que l'on note \(\mathrm {div}\vec B (M) \) défini par la formule d'Ostrogradski :
  \(\oiint_\mathfrak{S} \vec {B}(M_\mathfrak{S}) = \iiint_\mathfrak{V} \mathrm{div} \vec {B}(M_\mathfrak{V}) \mathrm{d}\mathfrak{V}(M_\mathfrak{V})\)
  \(M_\mathfrak{S}\) étant un point de la surface fermée \(\circledS\) et \(M_\mathfrak{V}\) un point du volume \((\mathfrak{V})\) délimité par \(\circledS\).
- Le flux du champ vectoriel \(\vec B (M)\) à travers une surface fermée quelconque \(\circledS\) est égal à l'intégrale triple du champ scalaire \(\mathrm{div} \vec B(M)\) étendue au volume \((\mathfrak{V})\) délimité par \(\circledS\) .
- L'opérateur divergence fait correspondre un champ vectoriel \(\vec B (M)\) à un champ de scalaire \(\mathrm{div} \vec B(M)\) ; il peut donner des informations sur le caractère "divergent ou convergent" du champ vectoriel \(\vec B (M)\) .
- Expressions de divergence de \(\vec B(M)\) dans différents systèmes de repérage.
  Repérage cartésien : \(\mathrm{div} \vec B (M) = \frac {\partial B_x}{\partial x} + \frac {\partial B_y}{\partial y} + \frac {\partial B_z}{\partial z}\)
  Repérage cylindrique : \(\mathrm{div} \vec B (M) = \frac 1{\rho} \frac {\partial(\rho B_\rho)}{\partial \rho} + \frac 1{\rho} \frac {\partial B_\varphi}{\partial \varphi} + \frac{\partial B_z}{\partial z}\)
  Repérage sphérique : \(\mathrm{div} \vec B (M) = \frac 1{r^2} \frac {\partial(r^2 B_r) }{\partial r} + \frac 1{r \sin \theta} \frac {\partial(B_\theta \sin \theta)}{\partial \theta} + \frac 1{r \sin \theta} \frac {\partial B_\varphi} {\partial \varphi}\)