Représentation mathématique de notions physiques

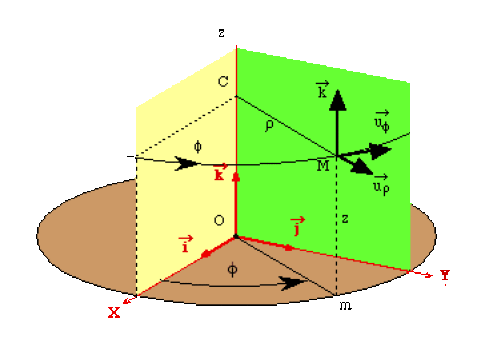
La base \((\overrightarrow{u_\rho},\overrightarrow{u_\Phi},\vec k)\) et les coordonnées \((\rho, \Phi,z)\) sont définies comme suit :

Soit \(m\) la projection de \(M\) sur le plan \((xOy)\).

• \(\rho = Om = CM\) toujours \(> 0\)

• \(\Phi=(\overrightarrow{OX}, \overrightarrow{Om})\)

• \(z = OC = mM\)

Si on fixe \(\Phi\) et \(z\) en faisant varier \(\rho\), \(M\) décrit la droite \(CM\) :

• La ligne coordonnée associée à \(\rho\) est une droite.

• La ligne coordonnée associée à \(\Phi\) est un cercle de centre \(C\), de rayon \(CM\), tracé dans un plan parallèle à \((xO_y)\).

• Enfin la ligne coordonnée associée à \(z\) est une droite \(mM\) toujours parallèle à \(O_z\).

L'animation ci-dessous montre l'ensemble du repérage cylindrique : la base, et les coordonnées

L'animation ci-dessous montre l'ensemble du repérage cylindrique : de la base, des coordonnées et de leurs accroissements élémentaires

Les vecteurs de base sont constamment tangents aux lignes coordonnées.

Ils sont orientés dans le sens croissant de la coordonnée correspondante : \(\overrightarrow{u_\rho}\) dans le sens de \(\rho\) croissant, \(\overrightarrow{u_\Phi}\) dans le sens de \(\Phi\) croissant,\(\vec k\) dans le sens de \(z\) croissant.

Ils forment une base orthonormée directe et la direction de \(\overrightarrow{u_\rho}\) et \(\overrightarrow{u_\Phi}\) dépend du point \(M\).

C'est pourquoi la base des coordonnées polaires cylindriques est dite base locale. \(\overrightarrow{OM}=\overrightarrow{Om}+\overrightarrow{mM}\)

Le vecteur position s'exprime alors dans la base cylindrique : \(\overrightarrow{OM}=\rho\overrightarrow{u_\rho}+z\overrightarrow{k}\)