Lois de la réflexion
Durée : 10 mn
Note maximale : 5
Question
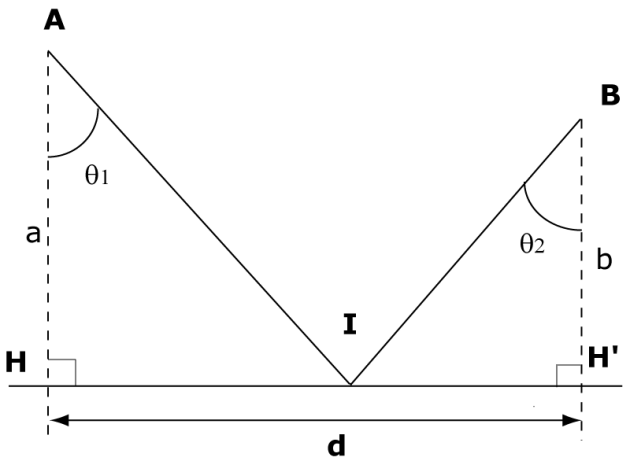
Un homme doit parcourir le chemin \(AIB\) à la vitesse \(V\).
Trouver la relation entre les angles \(\theta_1\) et \(\theta_2\) pour que le temps de parcours soit minimum (\(a, b\) et \(d\) sont donnés).
Solution
Calculons le temps nécessaire pour parcourir le chemin \(AIB\):
\(t=\frac{AI}V+\frac{IB}V\)(1 pt)
\(AI=(a^2+x^2)^{1/2}\)
\(IB=(b^2+(d-x)^2)^{1/2}\)
\(t=\frac1V\left[(a^2+x^2)^{1/2}+(b^2+(d-x)^2)^{1/2}\right]\)(1 pt)
dérivons la variable temps par rapport à la distance variable \(x\) soit :
\(\frac{dt}{dx}=\frac1V\left[\frac x{(a^2+x^2)^{1/2}}-\frac{d-x}{(b^2+(d-x)^2)^{1/2}}\right]\)
\(\displaystyle{\sin\theta_1=\frac x{(a^2+x^2)^{1/2}}}\) et \(\sin\theta_2=\frac{d-x}{(b^2+(d-x)^2)^{1/2}}\)
on en déduit : \(\frac{dt}{dx}=\frac1V(\sin\theta_1-\sin\theta_2)\) (2 pts)
le temps de parcours passera par un minimum si la dérivée s'annule, soit si :
\(\frac{dt}{dx}=0\) alors : \(\sin\theta_1=\sin\theta_2\) ; on en déduit : \(\theta_1=\theta_2\)(1 pt)
ce qui constitue la 1ère loi de la réflexion de Descartes.