Lois de la réfraction
Durée : 6 mn
Note maximale : 5
Question
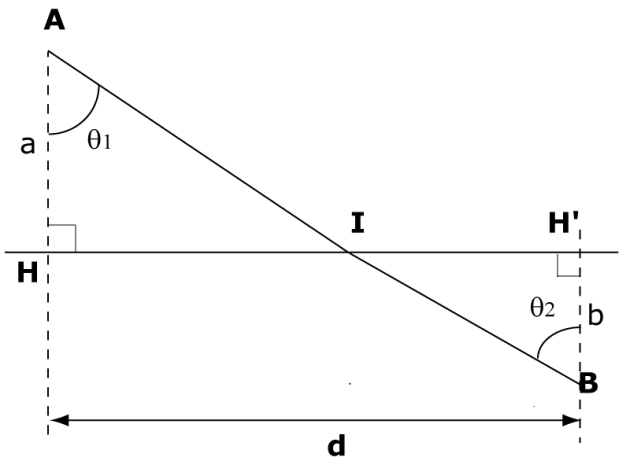
Un homme part du point \(A\) pour sauver un nageur qui se noie en \(B\). Il court de \(A\) en \(I\) à la vitesse \(V_1\) et nage de \(I\) à \(B\) à la vitesse \(V_2\).
Déterminer par l'intermédiaire des angles \(\theta_1\) et \(\theta_2\) la position de \(I\) pur que le temps mis pour aller de \(A\) à \(B\) soit minimum (\(a, b\) et \(d\) sont donnés).
Retrouver à l'aide de ces résultats les lois de Descartes.
Solution
calculons dans ce cas le temps mis pour aller de \(A\) en \(B\) :
\(t=\frac{AI}{V_1}+\frac{IB}{V_2}\) (1 pt)
\(t=\frac1{V_1}\cdot(a^2+x^2)^{1/2}+\frac1{V_2}\cdot(b^2+(d-x)^2)^{1/2}\) (1 pt)
calculons la dérivée par rapport à \(x\) :
\(\frac{dt}{dx}=\frac{1}{V_{1}}\cdot \frac {x}{(a^{2}+x^{2})^{1/2}}+\frac{1}{V_{2}}\cdot \frac{d-x}{(b^{2}+(d-x)^{2})^{1/2}}\)
\(\frac{dt}{dx}=\frac{\sin\theta_1}{V_1}-\frac{\sin\theta_2}{V_2}\)
cette dérivée s'annule : pour
\(\frac{dt}{dx}=0\) si \(\frac{\sin\theta_1}{V_1}=\frac{\sin\theta_2}{V_2}\) (2 pts)
Retrouvons à l'aide de ces résultats les lois de Descartes.
on a : \(\frac{\sin\theta_1}{V_1}=\frac{\sin\theta_2}{V_2}\)
en multipliant chaque membre par \(c\) : \(\frac c{V_1}\cdot\sin\theta_1=\frac c{V_2}\cdot\sin\theta_2\)
si l'on définit \(n\) par : \(n = \frac{c}{V}\) alors :
\(n_1\cdot\sin\theta_1=n_2\cdot\sin\theta_2\) (1 pt)
ce qui constitue la loi de la réfraction.