Réflexions sur les faces d'un prisme
Durée : 10 mn
Note maximale : 5
Question
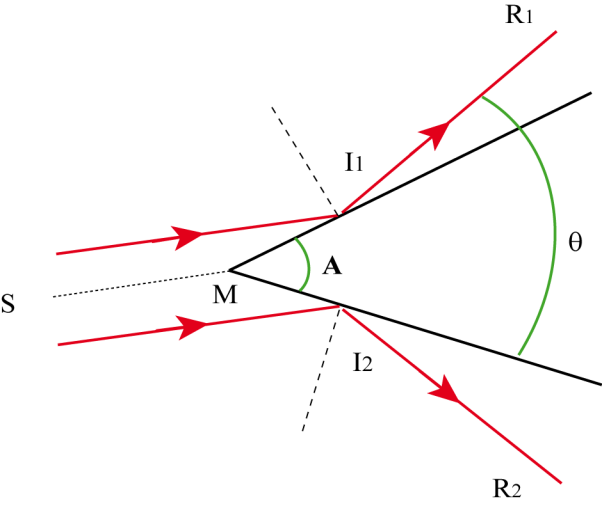
Un faisceau de rayons parallèles arrive perpendiculairement à l'arête d'un prisme d'angle \(A\) en verre d'indice \(n\).
Montrer que les rayons réfléchis \(I_1R_1\) et \(I_2R_2\) font entre eux un angle \(\theta =2A\). La direction de l'axe du faisceau \(S_0M\) est-elle importante par rapport au résultat précédent ?
Solution
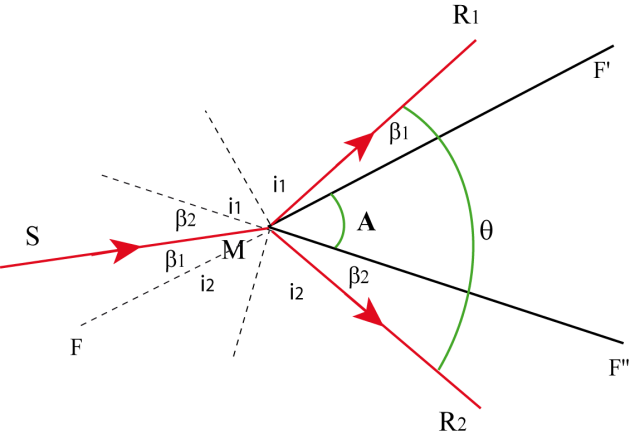
Considérons le rayon incident \(S_0M\) sur l'arête du prisme : il se réfléchit en \(MR_1\) et \(MR_2\). En appliquant la loi de la réflexion pour \(R_1\) on déduit : \(S_0MF=R_1MF'=\beta_1\) et donc
\(S_0MF=F'MS'=\beta_ 1\) comme angles opposés par le sommet.
En faisant le même raisonnement sur \(R_2\) on en déduit : \(S'MF''=\beta_2\).
Evaluons \(\theta : \theta =R_1MF'+F'MS'+S'MF''+F''MR_2\)
soit \(\theta=\beta_1+\beta_1+\beta_2+\beta_2=2(\beta_1+\beta_2)\)
or \(A=\beta_1+\beta_2\) donc finalement : \(\theta =2A\) (3 pts)
La direction de l'axe du faisceau \(S_0M\) est-elle importante par rapport au résultat précédent ?
\(i_1\) et \(i_2\) sont supérieurs à l'angle limite et les rayons incidents subissent une réflexion totale. La direction de l'axe du faisceau incident \(S_0M\) n'intervient pas. (2 pts)