Positionnement d'un miroir plan
Durée : 6 mn
Note maximale : 5
Question
Une femme mesurant 1,60m se tient debout devant un miroir plan vertical.
Quelle est la hauteur minimale du miroir et à quelle hauteur du sol doit se trouver le bord inférieur du miroir pour que la femme puisse se voir des pieds à la tête (on supposera que ses yeux se situent à 10 cm au dessous du sommet de son crâne.
Indiquer également à quelle distance par rapport au miroir cette personne doit se situer pour répondre à la situation envisagée précédemment.
Solution
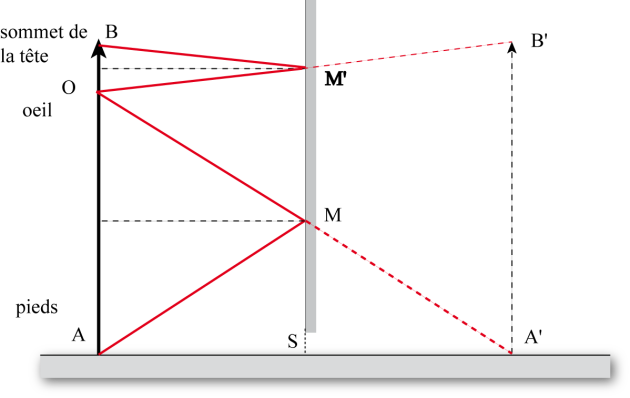
Pour que la personne puisse se voir en entier par réflexion sur le miroir il faut qu'un rayon, issu du sommet de sa tête \(B\), passe après réflexion sur le miroir par son oeil \(O\). De même un rayon issu de ses pieds \(A\) doit également après réflexion sur le miroir passer par son oeil. Ce qui conduit à la figure ci-contre où les rayons \(BM'O\) et \(AMO\) ont été tracés en tenant compte des lois de la réflexion. Nous voyons donc qu'il est possible de limiter la hauteur du miroir à la distance \(MM'\) puisque la partie extérieur à \(MM'\) n'interviendra pas dans le cheminement des rayons réfléchis. (2 pts)
Calculons \(MM'\) : \(M\) est situé sur la médiatrice de \(OA\) donc :
\(MS=\frac{AO}2=\frac{1,6-0,1}2=0,75m\)
de même \(M'\) est situé sur la médiatrice de \(OB\) donc :
\(SM'=AB-\frac{OB}2=1,6-\frac{0,1}2=1,55m\)
ce qui nous permet de déduire \(MM'\) :
\(MM'=SM'-SM=1,55-0,75=0,8m\)(2 pts)
Nous n'avons pas eu besoin de préciser la position du miroir par rapport à la personne pour conduire le raisonnement précédent. La valeur de \(MM'\) trouvée est indépendante de la position du miroir par rapport à l'observateur. (1 pt)