Lentilles minces

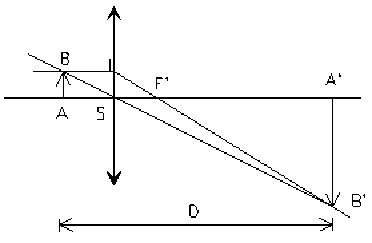
géométriquement on voit que :

\(\frac{SA}{SA'}=\frac{AB}{A'B'}=\frac{1}4\)

or \(AA'=AS+SA'=AS+4 \quad AS=5\quad AS=D\)

\(AS=\frac D5=\frac55=1\textrm m\)

et \(SA'=4\textrm m\)

d'autre part :

\(\frac{A'B'}{AB}=\frac{F'A'}{F'S}=\frac{F'A'}f=4=\frac{SA'-f}f=4\)

soit : \(SA' - f = 4 f\) et \(SA' = 5f\)

\(f=\frac{SA'}5=\frac{4}5=0,8\textrm m\) (1 pt)

Utilisons maintenant les formules de conjugaison :

\(\frac1{\overline{SA'}}-\frac1{\overline{SA}}=\frac1{\overline{SF'}}\) et \(\gamma=\frac{\overline{SA'}}{\overline{SA}}\)

\(\overline{SA'}=\gamma.\overline{SA}\)

\(\overline{AA'}=D=\overline{AS}+\overline{SA'}=-\overline{SA}+\gamma.\overline{SA}=(\gamma-1)\overline{SA}\)

d'où \(\overline{SA}=\frac D{\gamma-1}=\frac5{-4-1}=-1\textrm m\)

\(\overline{SA'}=\gamma.\overline{SA}=\frac\gamma{\gamma-1}D\)

soit : \(\overline{SA'}=4m\) ; on en tire :

\(\frac1{\overline{SF'}}=\frac{\gamma-1}{\gamma.D}-\frac{\gamma-1}D=\frac{\gamma-1}D\left(\frac1\gamma-1\right)=-\frac{(\gamma-1)^2}{\gamma.D}\)

\(\overline{SF'}=-\frac\gamma{(\gamma-1)^2}D=-\frac{-4}{(-5)^2}\cdot5=0,8\textrm m\)

\(\overline{SF'}=-\overline{SF}=0,8\textrm m\) (1 pt)