Rayon de courbure d'une lentille
Durée : 5 mn
Note maximale : 2
Question
Une lentille biconvexe a deux faces de même rayon de courbure \(R\) (\( R > 0\) ). Elle donne d'un objet \(AB\) de 5 cm, réel placé à 75 cm de la lentille, une image réelle à 150 cm de la lentille. On donne l'indice \(n\) du verre de la lentille ( \(n = 1,45\) ) .
Calculer \(R\)
Solution
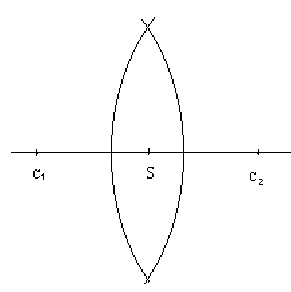
nous avons : \(\frac1{\overline{SA}}-\frac1{\overline{SA'}}=\frac1{\overline{SF'}}\)
\(\frac1{\overline{SF'}}=(n-1)\left(\frac1{\overline{SC_1}}-\frac1{\overline{SC_2}}\right)\) (1 pt)
or \(\overline{SC_1}=R=-\overline{SC_2}\)
\(\frac1{\overline{SF'}}=(n-1)\frac2R=\frac1{\overline{SA}}-\frac1{\overline{SA'}}\)
on en déduit la valeur de \(R\) :
\(R=\frac{2(n-1)}{\frac1{\overline{SA}}-\frac1{\overline{SA'}}}=\frac{2(1,45-1)}{\frac1{0,75}-\frac1{1,5}}=1,35\textrm m\) (1 pt)