Lentille mince et miroir plan (2)
Durée : 5 mn
Note maximale : 2
Question
Un objet \(AB\) est placé à une distance x devant une lentille convergente de focale f. On place derrière cette lentille un miroir plan, à une distance d de la lentille.
Tracer et déterminer algébriquement l'image \(A'B'\) de \(AB\) par le système lentille-miroir-lentille pour \(x = f\) ; \(d = f\).
Solution
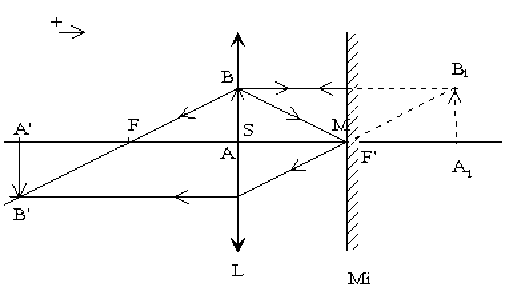
(image 1pt)
\(x=0 ; d=f\)
Déterminons algébriquement la position A' de l'image du point A :
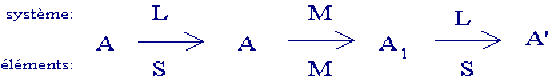
pour le miroir on a :
\(\overline{MA}=-\overline{MA_1}\)
pour la lentille, le sens de la lumière a changé et on a :
\(\frac{1}{\overline{SA'}}-\frac{1}{\overline{SA_1}}=\frac{1}{\overline{SF}}\)
\(\frac{1}{\overline{SA'}}=\frac{1}{\overline{SA_1}}+\frac{1}{\overline{SF}}\)
\(\overline{SA_1}=\overline{SM}+\overline{MA_1}=\overline{SF'}+(-\overline{MA})=\overline{SF'}+\overline{SF'}=2\overline{SF'}=-2\overline{SF}\)
d'où \(\frac{1}{\overline{SA'}}=-\frac{1}{2\overline{SF}}+\frac{1}{\overline{SF}}=\frac{1}{2\overline{SF}}\)
soit : \(\overline{SA'}=2\overline{SF}\) (1pt)