Association de systèmes centrés : distance focale
Partie
Question
Etablir la position algébrique \(\overline{F_1F}\) du point principal objet \(H\) d'une association \((S)\) de deux systèmes \((S_1)\) et \((S_2)\) à l'aide de l'expression du grandissement transversal.
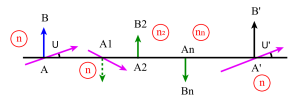
On désignera par \(X_{on}\) la coordonnée d'un point objet, origine prise au foyer objet du système \(n\).
Connaissant la position \(\overline{F_1F}=(f_1\cdot f'_1)/\Delta\) du foyer objet \(F\), en déduire la distance focale objet de l'association de deux systèmes en fonction de leurs distances focales objet respectives et de leur intervalle optique \(\overline{F'_1F_2}=\Delta\).
Utiliser la relation donnant le grandissement.
Aide simple
L'image d'un petit objet debout en \(H\) a, par définition, même taille, même sens que l'objet.
Aide détaillée
Le grandissement transversal d'un petit objet \(AB\) debout sur l'axe en \(H\) peut s'écrire :
\(\gamma=\frac{\overline{A'B'}}{\overline{AB}}=\frac{\overline{A'B'}}{\overline{A'_1B'_1}}\times\frac{\overline{A'_1B'_1}}{\overline{AB}}=(\gamma)_{S_2}\times(\gamma)_{S_1}=1\)
Rappel de cours
Relation de Lagrange-Helmholtz entre l'objet \(AB\) et son image \(A'B'\) :
\(n\overline{AB}u=n'\overline{A'B'}u'\)
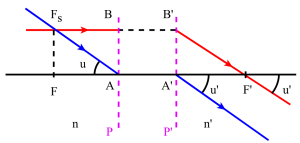
Les plans principaux sont deux plans de front conjugués : le plan principal objet et le plan principal image pour lesquels le grandissement linéaire (ou transversal) est égal à +1.
Relation entre les distances focales objet \(f\) et image \(f'\) :
\(\frac{f'}{f}=-\frac{n'}n\)
La vergence d'un système centré sera défini par :
\(V=\frac{n'}{f'}=-\frac nf\)
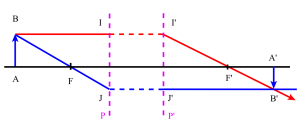
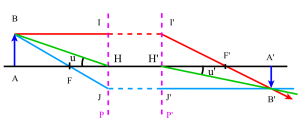
Construction de l'image d'un objet plan. On utilisera 2 rayons particuliers :
l'un issu de \(B\) et parallèle à l'axe optique : il émerge après le plan principal image en passant par le foyer image \(F'\)
l'autre issu de \(B\) et passant par le foyer objet \(F\) : il émerge après le plan principal image, parallèle à l'axe optique
Construction de l'émergent correspondant à un incident quelconque. On utilisera les mêmes rayons particuliers que ceux qui ont servi à construire l'image d'un objet \(AB\).
Formules de conjugaison :
Origine aux points principaux :
si : \(\overline{HA}=p\) et \(\overline{H'A'}=p'\) : \(\frac fp+\frac{f'}{p'}=1\) \(\frac{n'}{p'}-\frac np=\frac{n'}{f'}=C\) avec C vergence du système.
Origine aux foyers: formules de Newton :
si \(\overline{FA}=x\) et \(\overline{F'A'}=x'\) : \(\begin{array}{l}x\cdot x'=f\cdot f'\\\gamma=\frac{\overline{A'B'}}{\overline{AB}}=-\frac fx=-\frac{x'}{f'}\end{array}\)
grandissement angulaire : \(G=\frac{u'}u=\frac n{n'}\frac{\overline{AB}}{\overline{A'B'}}\)
produit du grandissement linéaire par le grandissement angulaire : \(\gamma\cdot G=\frac n{n'}\)
Les plans antiprincipaux sont deux plans conjugués entre lesquels le grandissement est égal à -1. Ce sont les symétriques des plans principaux par rapport aux foyers correspondants (de même pour les plans antiprincipaux).
Les points nodaux \(N\) et \(N'\) sont deux points conjugués, situés sur l'axe, et tels qu'à tout rayon incident passant par le point nodal objet, corresponde un rayon émergent passant par le point nodal image et parallèle au rayon incident.
Les éléments cardinaux d'un système centré comportent: les foyers, les points principaux et antiprincipaux, les points nodaux et antinodaux.
Lorsque pour un système centré donné on connaît deux couples d'éléments cardinaux ou un couple et une distance focale alors le système centré est parfaitement défini.
Solution détaillée
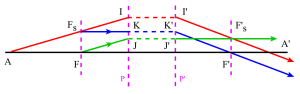
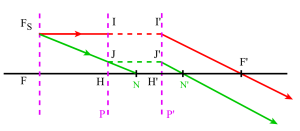
Si \(A'_1\) est l'image du point \(A\) de l'axe par le système (1) et \(A'\) l'image de \(A'_1\) par le système (2), le grandissement transversal \(g\) d'un petit objet \(AB\) debout sur l'axe en \(H\) peut s'écrire :
\(\gamma=\frac{\overline{A'B'}}{\overline{AB}}=\frac{\overline{A'B'}}{\overline{A'_1B'_1}}\times\frac{\overline{A'_1B'_1}}{\overline{AB}}=(\gamma)_{S_2}\times(\gamma)_{S_1}=1\)
\(g=1\) entraine \(A\equiv H\). En utilisant \((\gamma)_{S_1}=-\frac{f_1}{X_{01}}=\frac{-f_1}{\overline{F_1A}}\) et \((\gamma)_{S_2}=-\frac{f_2}{\overline{F_2A'_1}}-\frac{f_2}{X_{02}}\)
\(\gamma=\frac{f_1\cdot f_2}{X_{01}\cdot X_{02}}=1\)® \(X_{01}=\overline{F_1A}=\overline{F_1H}\)
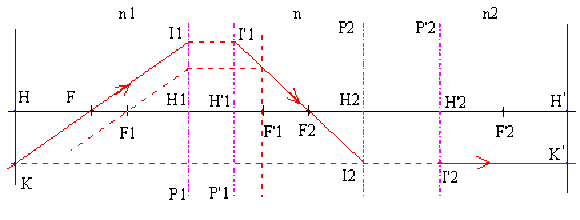
L'image \(A'_1\) fournie par le premier système est perçue comme un objet par le second système, soit :
\(X_{02}=\overline{F_2A'_1}=\overline{F_2F'_1}+\overline{F'_1A'_1}=-\overline{F'_1F_2}+\overline{F'_1A'_1}=-\Delta+X'_{01}\)
ou encore avec l'équation de Newton \(X_{01}.X'_{01}=f_1\cdot f'_1 :X_{02}=-\Delta+\frac{f_1\cdot f'_1}{X_{01}}\)
d'où : \(\gamma=\frac{f_1\cdot f_2}{X_{01}\left(-\Delta+\frac{f_1\cdot f'_1}{X_{01}}\right)}=1\) ou \(f_1.f_2=-X_{01}\cdot\Delta+f_1\cdot f'_1\) (car \(f_1/f'_1=-1\))
soit \(X_{01}=+\frac{f_1(f'_1-f_2)}\Delta\) or \(X_{01}=\overline{F_1H}\) et \(\overline{F_1F}=\frac{f_1f'_1}\Delta\)
d'où \(\overline{HF}=f=\overline{HF_1}+\overline{F_1F}=\frac{-f_1(f'_1-f_2)}\Delta+\frac{f_1f'_1}\Delta=\frac{f_1\cdot f_2}\Delta\)
et \(f=\overline{HF}=\frac{f_1f_2}{\overline{F'_1F_2}}\)