Foyer image
Partie
Question
Deux systèmes centrés convergents, d'une dioptrie, ont été réalisés avec les doublets suivants :
système 1

\(f'_1 = 0,2 \textrm m\) \(f'_2 = 0,2 \textrm m\) \(\Delta=\overline{F'_1F_2}= - 0,04 \textrm m\)
système 2

\(f'_1 = 0,2 \textrm m\) \(f'_2 =- 0,2 \textrm m\) \(\Delta=\overline{F'_1F_2}= + 0,04 \textrm m\)
L'image, par ces systèmes, d'objets très éloignés (supérieure à 1000 fois le module de la distance focale) peut elle être recueillie sur une pellicule photographique ?
Vérifier schématiquement le résultat trouvé.
Où est située l'image d'un objet très éloigné ?
Aide simple
L'image d'un objet très éloigné est pratiquement dans le plan focal image.
Quel que soit le système centré utilisé, une pellicule photographique ne peut recevoir une image que si celle-ci est réelle.

Aide détaillée
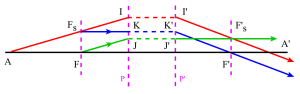
L'image par \(L_1\) d'un point de l'axe à l'infini est en \(F'_1\). Le foyer image \(F'\) d'un doublet de lentilles \((L_1)\), \((L_2)\) est donc toujours l'image par la seconde lentille du foyer image \(F'_1\) de la première.
Soit avec la relation de Newton : \(\overline{F_2F'_1}\cdot\overline{F'_2F'}=\overline{f_2f'_2}=-f^2_2\).

Rappel de cours
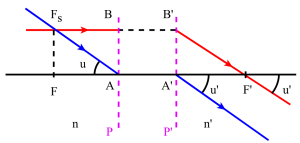
Les plans principaux sont deux plans de front conjugués : le plan principal objet et le plan principal image pour lesquels le grandissement linéaire (ou transversal) est égal à +1.
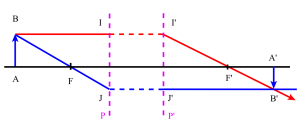
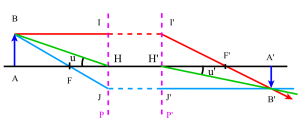
Construction de l'image d'un objet plan. On utilisera 2 rayons particuliers :
l'un issu de \(B\) et parallèle à l'axe optique : il émerge après le plan principal image en passant par le foyer image \(F'\)
l'autre issu de \(B\) et passant par le foyer objet \(F\) : il émerge après le plan principal image, parallèle à l'axe optique
Formules de conjugaison :
Origine aux foyers: formules de Newton :
si \(\overline{FA}=x\) et \(\overline{F'A'}=x'\) : \(\begin{array}{l}x\cdot x'=f\cdot f'\\\gamma=\frac{\overline{A'B'}}{\overline{AB}}=-\frac fx=-\frac{x'}{f'}\end{array}\)
grandissement angulaire : \(G=\frac{u'}u=\frac n{n'}\frac{\overline{AB}}{\overline{A'B'}}\)
produit du grandissement linéaire par le grandissement angulaire : \(\gamma\cdot G=\frac n{n'}\)
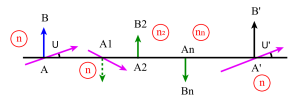
Les plans antiprincipaux sont deux plans conjugués entre lesquels le grandissement est égal à -1. Ce sont les symétriques des plans principaux par rapport aux foyers correspondants (de même pour les plans antiprincipaux).
Les éléments cardinaux d'un système centré comportent: les foyers, les points principaux et antiprincipaux, les points nodaux et antinodaux.
Lorsque pour un système centré donné on connaît deux couples d'éléments cardinaux ou un couple et une distance focale alors le système centré est parfaitement défini.
Solution détaillée
1.1) L'image d'objet très éloignés se forme dans le plan focal image. Elle pourra être recueillie sur une pellicule photographique si le plan focal image a une position d'image réelle. Calculons la position du foyer image du système (1)

\(\overline{F'_1F_2}=-0,04\textrm m\)
\(\overline{F'_2F'}=-\frac{{f'_{2}}^{2}}{\overline{F_2F'_1}}=\frac{-(0,04\textrm m^{2})}{0,04\textrm m}=-1\textrm m\)

Le foyer image \(F'\) de ce système est à 1 mètre à gauche du foyer image de \((L_2)\), il est virtuel. Il n'y aura pas d'image réelle d'objet très éloigné. Ce dispositif ne peut servir d'objectif photographique.
1.2) Position du foyer image du système (2)

\(\overline{F'_1F_2}=+0,04\textrm m\)
\(\overline{F'_2F'}=-\frac{{f'_{2}}^{2}}{\overline{F_2F'_1}}=\frac{-(0,04\textrm m^{2})}{-0,04\textrm m}=+1\textrm m\)

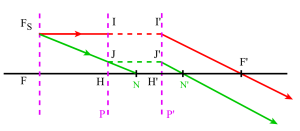
Le foyer image \(F'\) de ce système est à 1 mètre à droite du foyer image de \((L_2)\) soit à 0,8m de son centre \(O_2\). Ce foyer image est réel. On peut y placer un film.
2) Vérification
Le film, surface sensible à la lumière, doit être au delà de \(O_2\), il ne peut être en \(F'\) qui est virtuel. L'association proposée des 2 lentilles convergentes ne peut servir d'objectif photographique.

L'image d'un objet à l'infini peut être recueillie sur un film au foyer image \(F'\) parce que ce dernier est réel.