Dioptre sphérique équivalent à l'oeil au repos
Partie
Question
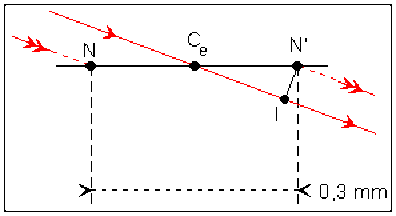
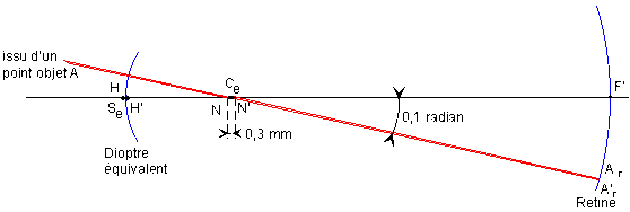
Les plans principaux et les points nodaux de l'oeil sont tels que \(\overline{HH'}=\overline{NN'}=0,3\textrm{mm}\) et \(\overline{HN}=6\textrm{mm}\).
Vérifier géométriquement et algébriquement qu'il existe un dioptre sphérique équivalent à l'œil au repos. Cette équivalence sera supposé établie si ce dioptre donne d'un point objet infiniment éloigné à 0,1 radian de l'axe, un point image sur la rétine à moins de 0,015 mm du point image que fournirait l'oeil réel.
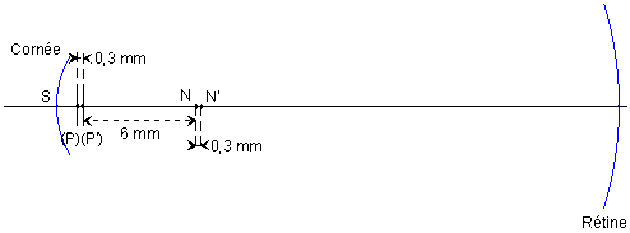
Eléments d'enveloppe et éléments cardinaux de l'oeil réel.
Revoir les éléments cardinaux du dioptre sphérique (points principaux et nodaux)
Aide simple
Les points principaux \(H\) et \(H'\) d'un dioptre unique sont confondus avec le sommet \(S\) de ce dioptre.
Les points nodaux \(N\) et \(N'\) d'un dioptre unique sont confondus avec le centre de courbure \(C\) de ce dioptre.
Aide détaillée
Tout dioptre sphérique a ses points nodaux \(N, N'\) confondus avec son centre de courbure et ses plans principaux confondus avec le plan tangent au sommet du dioptre.
Le dioptre sphérique équivalent, s'il existe, doit avoir son sommet au milieu du segment \(HH'\) et son centre au milieu du segment \(NN'\) de l'oeil.
Calculez la distance entre le point image réel \(A_r\) fourni par l'oeil et le point image \(A'_r\) qui serait fourni par le dioptre équivalent.
Rappel de cours
Le dioptre sphérique n'est rigoureusement stigmatique que pour les points de sa surface et son centre.
Il y a stigmatisme approché pour tout point de l'espace qui n'envoie sur le dioptre sphérique qu'un pinceau lumineux dont le rayon moyen lui est normal, c'est à dire peu incliné par rapport à l'axe du dioptre ou encore formé de rayons paraxiaux. Tout rayon incident parallèle à l'axe optique se réfracte en passant par le foyer image \(F'\).
Un rayon incident passant par le foyer objet du dioptre se réfractera en un rayon parallèle à l'axe optique du dioptre.
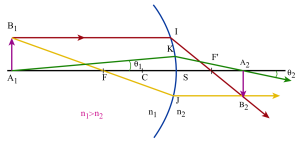
Pour construire l'image d'un objet plan :
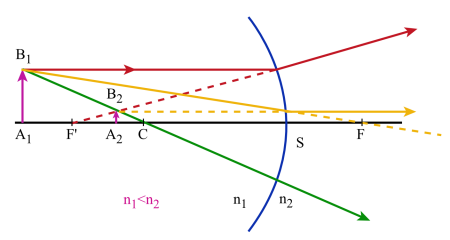
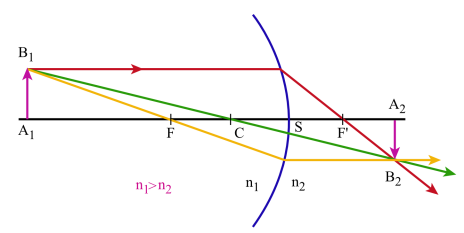
on utilise 3 rayons particuliers :
un rayon passant par le centre du dioptre et qui n'est pas dévié à la traversée de celui-ci
un rayon issu de \(B_1\) et passant par le foyer objet \(F\) : il est réfracté suivant une parallèle à l'axe principal
un rayon issu de \(B_1\) et parallèle à l'axe principal: il est réfracté suivant un rayon qui passe par le foyer image \(F'\).
Formules de conjugaison :
Origine au sommet
\(\frac{n_1}{\overline{SA_1}}-\frac{n_2}{\overline{SA_2}}=\frac{n_1-n_2}{\overline{SC}}\)
\(\gamma=\frac{n_1}{n_2}\frac{\overline{SA_2}}{\overline{SA_1}}\)
Origine au centre
\(\frac{n_1}{\overline{CA_2}}-\frac{n_2}{\overline{CA_1}}=\frac{n_1-n_2}{\overline{CS}}\)
\(\gamma=\frac{\overline{A_2B_2}}{\overline{A_1B_1}}=\frac{\overline{CA_2}}{\overline{CA_1}}\)
Origine aux foyers
\(\overline{FA_1}\overline{F'A_2}=\overline{SF}\overline{SF'}=ff'\)
\(\gamma=-\frac f{\overline{FA_1}}=\frac{\overline{F'A_2}}{f'}\)
Relation de Lagrange-Helmholtz :
Solution détaillée
Vérifions que le dioptre sphérique de centre \(C\), milieu de \(NN'\), de sommet \(S\), milieu de \(HH'\) dont la distance focale image serait égale à celle de l'oeil au repos (\(F'\) sur la rétine), remplit la condition posée.
Les rayons issus d'un point objet \(A\) infiniment éloignés sont parallèles lorsqu'ils arrivent sur la cornée. Dans l'œil réel l'image de \(A\) est sur la rétine à l'intersection du rayon parallèle au rayon incident passant par le point nodal image \(N'\). Dans le modèle du dioptre sphérique, cette image est à l'intersection de la rétine avec le rayon parallèle au rayon incident passant par \(C\).
La distance \(A_rA'_r\) de ces deux points images est
\(A_rA'_r=N'l=C_eN'\cdot\sin0,1<0,1\cdot CN'<0,015\textrm{mm}\).
L'oeil au repos peut donc, avec une bonne approximation, être remplacé par un dioptre unique.