Accommodation

Partie

Question

Définir le résultat et le mécanisme de l'accommodation de l'œil normal.

Construire, à l'aide du dioptre équivalent à l'œil, l'image d'un point situé au proximum, supposé à 6 cm de l'œil. En déduire le déplacement du foyer image \(F'\) de l’œil, lors de l'accommodation.

Où se fait l'image d'un objet dans l'œil ?

Aide simple

L'image d'un objet est-elle indépendante de la position de l'objet ?

Où se trouve le foyer image de l'oeil emmétrope au repos ?

Rappel de cours

  • Le dioptre sphérique n'est rigoureusement stigmatique que pour les points de sa surface et son centre.

  • Il y a stigmatisme approché pour tout point de l'espace qui n'envoie sur le dioptre sphérique qu'un pinceau lumineux dont le rayon moyen lui est normal, c'est à dire peu incliné par rapport à l'axe du dioptre ou encore formé de rayons paraxiaux. Tout rayon incident parallèle à l'axe optique se réfracte en passant par le foyer image \(F'\).

  • Un rayon incident passant par le foyer objet du dioptre se réfractera en un rayon parallèle à l'axe optique du dioptre.

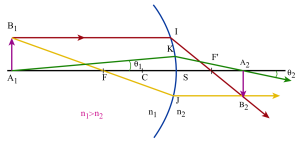
  • Pour construire l'image d'un objet plan :

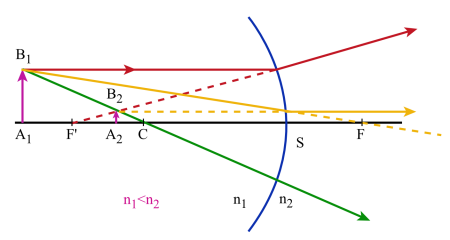
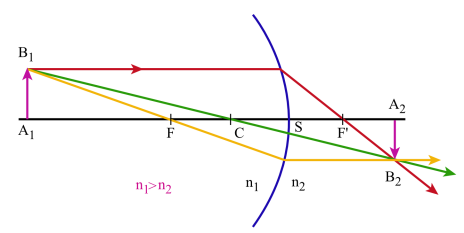
on utilise 3 rayons particuliers :

  • un rayon passant par le centre du dioptre et qui n'est pas dévié à la traversée de celui-ci

  • un rayon issu de \(B_1\) et passant par le foyer objet \(F\) : il est réfracté suivant une parallèle à l'axe principal

  • un rayon issu de \(B_1\) et parallèle à l'axe principal: il est réfracté suivant un rayon qui passe par le foyer image \(F'\).

Formules de conjugaison :

Origine au sommet

\(\frac{n_1}{\overline{SA_1}}-\frac{n_2}{\overline{SA_2}}=\frac{n_1-n_2}{\overline{SC}}\)

\(\gamma=\frac{n_1}{n_2}\frac{\overline{SA_2}}{\overline{SA_1}}\)

Origine au centre

\(\frac{n_1}{\overline{CA_2}}-\frac{n_2}{\overline{CA_1}}=\frac{n_1-n_2}{\overline{CS}}\)

\(\gamma=\frac{\overline{A_2B_2}}{\overline{A_1B_1}}=\frac{\overline{CA_2}}{\overline{CA_1}}\)

Origine aux foyers

\(\overline{FA_1}\overline{F'A_2}=\overline{SF}\overline{SF'}=ff'\)

\(\gamma=-\frac f{\overline{FA_1}}=\frac{\overline{F'A_2}}{f'}\)

Relation de Lagrange-Helmholtz :

\(n_1\overline{A_1B_1}\theta_1=n_2\overline{A_2B_2}\theta_2\)

Solution détaillée

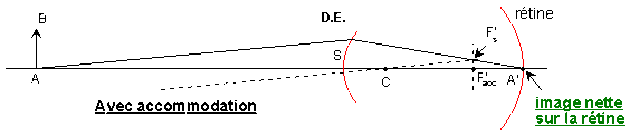
Le résultat de l'accommodation est le maintien du plan de l'image sur la rétine, lorsque la distance de l'objet, à l'œil, varie.

Le schéma ci-dessous démontre que l'accommodation est un raccourcissement de la distance focale image \(f'=\overline{SF'}\). Le foyer image \(F'\) se retrouve devant la rétine. Le mécanisme de l'accommodation est une augmentation de la vergence du cristallin par diminution de ses rayons de courbure.

La position connue de \(A'\) donne la position du foyer secondaire image \(F's\) et de \(F'\).