Définition du grossissement commercial
Partie
Question
Définir le grossissement commercial \(G_c\) d'un microscope, en fonction du grandissement transversal \(g\) fourni par l'objectif et le grossissement commercial \(g_c\) de l'oculaire.
\(G_c=\frac{\theta'}\theta\)
Reprendre la définition du grossissement
Aide simple
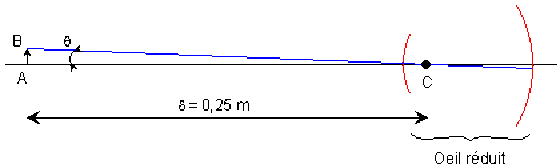
Le grossissement commercial \(G_c\) d'une loupe ou d'un microscope est le rapport entre l'angle \(\theta'\) sous-tendu par l'image à l'infini d'une très petite longueur \(AB\), et l'angle \(\theta\) sous-tendu par l'objet \(AB\) lorsqu'il est observé à la distance conventionnelle \(d =25 \textrm{cm}\).
Aide détaillée
Objectif et oculaire peuvent être schématisés par des lentilles minces.
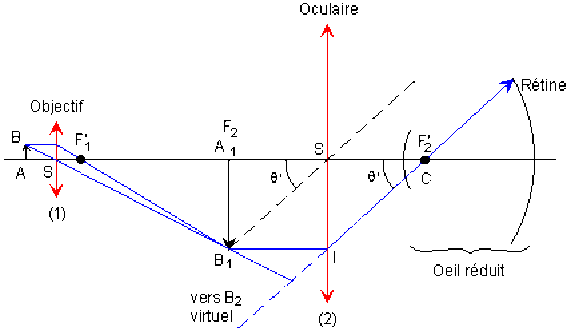
L'image fournie \(A_2B_2\) par l'oculaire est à l'infini si \(A_1B_1\) est dans le plan focal objet de l'oculaire : Si \(\theta'\) est petit \(\theta'\#\tan\theta'=\frac{A_2B_2}{CA_2}=\frac{SI}{SF'_2}=\frac{A_1B_1}{\left|f'_2\right|}\)
Attention : Le rayon émergent représenté n'est pas le rayon conjugué des rayons incidents mais un rayon de commodité qui fait bien apparaître \(\theta'\).
Rappel de cours
Un microscope permet d'observer les petits objets sous un angle plus grand qu'à l'œil nu.
Il se compose de deux systèmes de lentilles convergentes: l'objectif et l'oculaire.
L'objectif donne une image agrandie de l'objet, image qui est observée avec l'oculaire jouant le rôle de loupe.
Le grossissement d'un microscope se définit comme celui de la loupe : c'est le rapport entre l'angle \(\alpha'\) sous lequel on voit l'image de l'objet à travers la loupe et l'angle \(\alpha\) sous lequel on voit l'objet à l'oeil nu à la distance minimum de vision distincte : \(G=\frac{\alpha'}\alpha\)
Solution détaillée
Le grossissement commercial \(G_c\) d'une loupe ou d'un microscope est le rapport entre l'angle \(\theta'\) sous-tendu par l'image à l'infini d'une très petite longueur \(AB\), et l'angle \(\theta\) sous-tendu par l'objet \(AB\) lorsqu'il est observé à la distance conventionnelle \(d =25 \textrm{cm}\).
On suppose \(\theta\) et \(\theta'\) suffisamment petits pour écrire \(\theta\#\tan\theta\) et \(\theta'\#\tan\theta'\). Le grossissement commercial correspond à une observation de l'objet à l'oeil nu à la distance optimale conventionnelle de 0,25 m.

\(G_c=\frac{\theta'}\theta=\frac{A_1B_1}{\left|f'_2\right|}\times\frac{0,25}{AB}=(\gamma_{\textrm{obj}})\times\left(\frac{0,25\textrm m}{\left|f'_{OC}\right|}\right)\) car \(f'_2=f'_{\textrm{oculaire}}\)
\(G_c=\gamma_{\textrm{obj}}*g_c\)
Le grossissement commercial d'un microscope est égal au produit du grandissement transversal \(g\) de l'objectif par le grossissement commercial \(g_c\) de l'oculaire.