Puissance
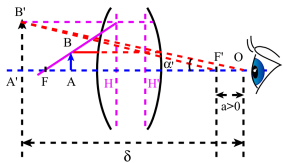
La puissance[1] est utilisée lorsque l'instrument donne une image virtuelle[2] d'un objet réel[3] à distance finie (loupe, oculaires positifs, microscope...).
La puissance de l'instrument est par définition : \(~P=\frac{\alpha'}{AB}\)
avec \(\alpha'\) exprimée en radians et \(P\) exprimé en dioptries lorsque \(AB\) est exprimé en m.
Posons : \(~\overline{H'F'}=f~\) et \(~\delta=OA'\)
nous avons alors :
\(\tan~\alpha'\approx\alpha'=\frac{A'B'}{OA'}=\frac{A'B'}{AB}~\frac{AB}{\delta}\)
\(P=\frac{\alpha'}{AB}=\frac{\gamma}{\delta}\)
si l'on applique la formule de Newton : \(~\gamma=\frac{A'B'}{AB}=-\frac f{\overline{FA}}=-\frac{\overline{F'A'}}f~\) on obtient :
\(P=\frac{F'A'}f~\frac1{\delta}=\frac1f~\frac{\delta~-~a}{\delta}\)
\(P=\frac1f~\Big(1~-~\frac a{\delta}\Big)\)
\(f\) et \(\delta\) sont positifs mais \(a\) peut être positif ou négatif suivant que l'oeil est au delà du foyer image[4] \(F'\) ou entre \(F'\) et la face de sortie du système. On voit donc que la puissance dépend de l'instrument par sa distance focale[1], de la position de l'oeil et de la mise au point. On définira la puissance intrinsèque \(P_i\) par :
\(P_i=\frac1f\)
Elle interviendra lorsque l'oeil est positionné au foyer image du système ou lorsque l'image \(A'B'\) est rejetée à l'infini.