Convention d'écriture des préfixes
Multiples et sous-multiples des unités \(\textrm{SI}\)
Les multiples et sous-multiples décimaux des unités de base et dérivées sont formés par l'utilisation de 20 préfixes auxquels sont associés noms et symboles :
Multiples | Sous-multiples | ||||
Facteur multiplicatif | Préfixe | Symbole | Facteur multiplicatif | Préfixe | Symbole |
\(10^{24}\) | yotta | \(\textrm{Y}\) | \(10^{-1}\) | déci | \(\textrm{d}\) |
\(10^{21}\) | zetta | \(\textrm{Z}\) | \(10^{-2}\) | centi | \(\textrm{c}\) |
\(10^{18}\) | exa | \(\textrm{E}\) | \(10^{-3}\) | milli | \(\textrm{m}\) |
\(10^{15}\) | peta | \(\textrm{P}\) | \(10^{-6}\) | micro | \(\mu\) |
\(10^{12}\) | téra | \(\textrm{T}\) | \(10^{-9}\) | nano | \(\textrm{n}\) |
\(10^{9}\) | giga | \(\textrm{G}\) | \(10^{-12}\) | pico | \(\textrm{p}\) |
\(10^{6}\) | méga | \(\textrm{M}\) | \(10^{-15}\) | femto | \(\textrm{f}\) |
\(10^{3}\) | kilo | \(\textrm{k}\) | \(10^{-18}\) | atto | \(\textrm{a}\) |
\(10^{2}\) | hecto | \(\textrm{h}\) | \(10^{-21}\) | zepto | \(\textrm{z}\) |
\(10\) | déca | \(\textrm{da}\) | \(10^{-24}\) | yocto | \(\textrm{y}\) |
Noms des préfixes
Les préfixes des multiples et sous-multiples décimaux sont choisis pour présenter les résultats numériques par des nombres de trois chiffres maximum.
Exemples :
\(20\) microampères pour \(\textrm{0,000 02}\) ampère
\(5\) millisecondes pour \(\textrm{0,005}\) seconde
\(\textrm{1,5}\) kilomètre pour \(1500\) mètres
Les préfixes qui ne correspondent pas à des puissances de \(10\) multiples de \(3\) sont à éviter, ce sont les centi \((\textrm{c})\), déci \((\textrm{d})\), déca \((\textrm{da})\) et hecto \((\textrm{h})\). Ces quatre préfixes sont habituellement associés au litre, et le dernier avec l'are \((10^{2}\textrm{m}^{2})\) forme l'hectare \((10^{4}\textrm{m}^{2})\)
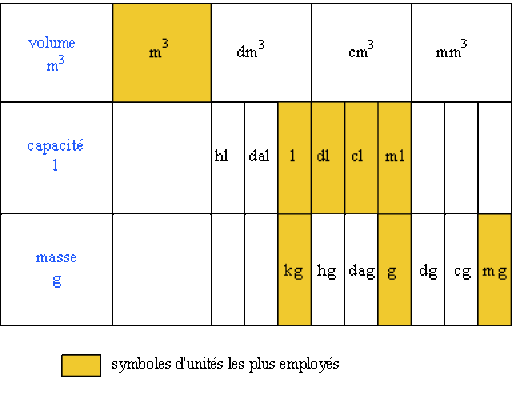
Le litre est un volume, approximatif de \(1\textrm{ dm}^{3}\) , occupé par un kilogramme d'eau à \(4^{\circ} \textrm{ C}\).
Les préfixes peuvent s'appliquer à des unités hors \(\textrm{SI}\) comme l'unité monétaire :
Exemples :
kilofranc = \(10^{3} \textrm{ F}\) ou \((\textrm{kF})\)
mégafranc = \(10^{6} \textrm{ F}\) ou \((\textrm{MF})\)
Les préfixes ne sont pas associés aux unités :
unités Hors \(\textrm{SI}\) : jours (\(\textrm{j}\) ou \(\textrm{d}\)), heure \((\textrm{h})\), minute \((\textrm{min})\), tour \((\textrm{tr})\), degré \((^{\circ})\), minute d'angle \((')\), seconde d'angle \((")\), quintal \((q)\).
unités \(\textrm{SI}\) : le "kilogramme" qui comprend déjà le préfixe kilo. Dans ce cas c'est au gramme que s'applique les préfixes.
Exemples :
Dire \(1 \textrm{ microgramme} = 1\mu\textrm{g} = 10^{-6} \textrm{ g} = 10^{-9}\textrm{ g}\) et non \(1\) \(\textrm{nanokilogramme}\).
L'association de deux préfixes par unité n'est pas autorisé
Exemples : Dire :
picoFarad \((\textrm{pF})\) et non millinanofarad \((\textrm{mnF})\)
micronewton-mètre \((\mu\textrm{Nm})\) et non millinewton-millimètre \((\textrm{mNmm})\)
gigagramme \((\textrm{Gg})\) et non mégakilogramme \((\textrm{Mkg})\)
Dans le cas où le nom de l'unité commence par une voyelle, le préfixe peut perdre sa dernière voyelle.
Exemples : Dire :
mégohm et non mégaohm
hectare et non hectoare
Un préfixe doit être associé à un nom d'unité. Ne pas dire et écrire un kilo, "comme on peut l'entendre et le voir auprès des détaillants de fruits et légumes" mais un kilogramme
Symboles des préfixes
Les symboles des préfixes, imprimés en caractères romains (droits) sont accolés aux symboles des unités.
Exemples :
\(1 \textrm{ nanoseconde} = 1 \textrm{ ns} = 10^{-9}\textrm{ s}\)
\(1 \textrm{ milliampère} = 1 \textrm{ mA} = 10^{-3} \textrm{ A}\)
\(1 \textrm{ gigaelectronvolt} = 1 \textrm{ Gev} = 10^{9} \textrm{ ev}\)
Le symbole d'un préfixe, combiné avec le symbole d'une unité \(\textrm{S.I.}\), constitue un nouveau symbole d'une nouvelle unité qui peut être élevée à une puissance.
Exemples :
\(1\textrm{ mm}^{3} = (10^{-3}\textrm{ m})^3 = 10^{-9}\textrm{ m}^{3}\)
\(1\textrm{ cm}^{-1} = (10^{-2}\textrm{ m})^{-1} = 10^{2} \textrm{ m}^{-1}\)
\(1 \textrm{ km}^{2} = (10^{3}\textrm{ m})^{2} = 10^{6}\textrm{ m}^{2}\)