Trigonométrie circulaire - Trigonométrie hyperbolique

La fonction cosinus hyperbolique, notée \(\textrm{ch}\) , est :

• définie sur \(\mathbb{R}\) : \(\textrm{ch }x = (e^{x} + e^{-x}) / 2\)

• paire : \(\textrm{ch }(-x) = \textrm{ch }x\)

Le domaine d'étude se réduit à \(D_{e} = [0, +\infty [\) . Le graphe de la fonction sinus hyperbolique, admet l'axe \(Oy\) comme axe de symétrie.

Aux bornes de \(D_{e}\), nous avons :

• \(\textrm{ch }0 = 1\)

• \(\displaystyle{\lim_{x \to + \infty} \textrm{ch}x \approx \lim_{x \to +\infty} e^{x} = + \infty}\)

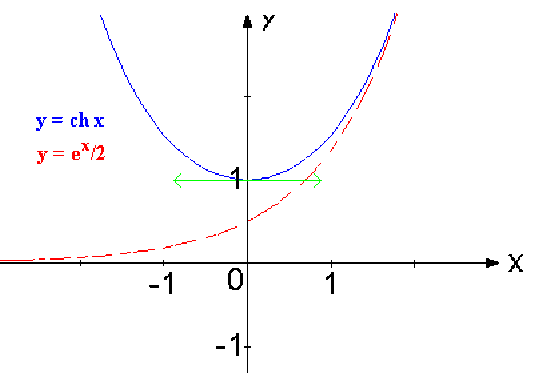
  avec \(\textrm{ch } x - e^{x}/2 = e^{-x} / 2 > 0\) (le graphe de \(\textrm{ch }x\) est asymptote en \(+\infty\) au graphe de la fonction \(y = e^{x} / 2\) et se trouve au-dessous de celui-ci).

La fonction dérivée \(\textrm{ch' }x = (e^{x} - e^{-x}) / 2 = \textrm{sh }x\) étant positive sur \(D_{e}\), la fonction \(\textrm{ch }x\) est croissante sur \(D_{e}\) .

Tableau de variation sur \(D_{e}\)

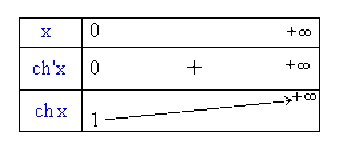
Représentation graphique de \(\textrm{ch }x\)