Adaptation en puissance - cellule LC
Partie
Question
On veut réaliser une adaptation en puissance entre un générateur de tension sinusoïdale de fréquence F et de résistance interne r, et une charge purement résistive de valeur \(R\).
Deux cas sont possibles :
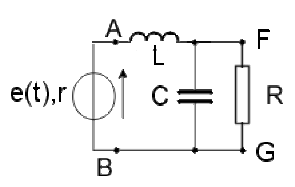
Figure a) : \(R> r\) ; montrer que ce montage permet de réaliser l'adaptation. Exprimer les valeurs à donner à \(L\) et \(C\) en fonction de \(r, R\) et \(\displaystyle{\omega = 2\pi\textrm F}\)
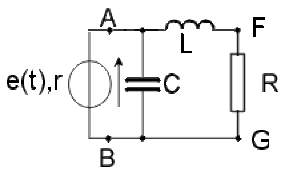
Figure b) : \(R< r\) ; montrer que ce montage permet de réaliser l'adaptation. Exprimer les valeurs à donner à \(L\) et \(C\) en fonction de \(r, R\) et \(\omega = 2\pi\textrm{F}\)
Aide simple
La puissance fournie par un générateur à une charge est maximale si leurs impédances complexes sont des complexes conjugués.
Aide détaillée
Pour que le transfert d'énergie soit optimal, il faut que le générateur soit adapté au circuit qu'il alimente. On peut donc chercher soit les conditions que doit vérifier le générateur pour fournir un maximum d'énergie à \(R\), ou, ce qui revient au même, les conditions que doit vérifier le circuit pour être adapté au générateur. Comme la puissance dissipée dans des éléments purement réactifs est nulle, toute l'énergie fournie par le générateur sera transmise à la charge \(R\).
D'où les deux méthodes :
Exprimer l'impédance interne complexe du générateur de Thévenin alimentant \(R\), et trouver la condition pour qu'elle soit le complexe conjugué de \(R\).
Exprimer l'impédance complexe du circuit alimenté par le générateur \(\{e(t), r\}\), et trouver la condition pour qu'elle soit le complexe conjugué de \(r\).
Aide méthodologique
Au choix :
Générateur de Thévenin équivalent à un réseau vu de deux bornes données.
Association mixte de dipôles.
Solution simple
a ] \(\displaystyle{(r < R)}\) \(\displaystyle{L=\frac{\sqrt{r(R-r)}}{\omega}}\); \(\displaystyle{C=\frac{1}{R\omega}\sqrt{\frac{R-r}{r}}}\)
b] \((r> R)\) \(\displaystyle{L=\frac{\sqrt{R(r-R)}}{\omega}}\) ; \(\displaystyle{C=\frac{1}{r\omega}\sqrt{\frac{r-R}{R}}}\)
Solution détaillée
a. \((r < R)\)
Calcul de l'impédance interne complexe du générateur de Thévenin alimentant \(R\).

L'impédance interne complexe du générateur de Thévenin alimentant \(R\) est celle du circuit vu des bornes \(F\) et \(G\), réduit à ses éléments passifs :

Ce circuit comporte deux branches en parallèle, l'une contenant le condensateur, et l'autre les deux autres dipôles, en série.
L'impédance complexe de dipôles associés en série est égale à la somme de leurs impédances complexes :
\(\displaystyle{Z_{RL} = Z_R +Z_L = R + jL\omega}\)
L'admittance complexe du dipôle équivalent à une association de dipôles en parallèle est égale à la somme des admittances complexes :
\(\displaystyle{\begin{array}{lll}\underline Y_{FG} & = & \underline Y_C+\underline Y_{rL}\\ & = & jC\omega+\frac{1}{r+jL\omega}\\ & = & \frac{(1-LC\omega^2)+jrC\omega}{r+jL\omega}\end{array}}\)
d'où l'impédance interne complexe du générateur :
\(\displaystyle{\underline Z_{FG}=\frac{1}{\underline Y_{FG}}=\frac{r+jL\omega}{(1-LC\omega^2)+jrC\omega}}\)
L'adaptation entre le générateur et sa charge est réalisée si leurs impédances complexes sont des complexes conjugués :
comme \(R\) est un réel,
\(\displaystyle{\underline Z_{FG}=R\frac{r+jL\omega}{(1-LC\omega^2)+jrC\omega}}\)
En identifiant les parties réelles, on obtient : \(\displaystyle{r=R(1 - LC\omega^2)}\) , égalité qui ne peut être vraie que si \(\displaystyle{LC\omega^2<1}\) ;
L'égalité des parties imaginaires donne \(R = rRC\);
en tirant \(C\) de cette relation et en le reportant dans la première, on obtient :
\(\displaystyle{L=\frac{\sqrt{r(R-r)}}{\omega}}\) , qui permet de tirer \(\displaystyle{C=\frac{1}{R\omega}\sqrt{\frac{R-r}{r}}}\) , solutions qui ne sont acceptables que si \(r < R\)
2 ] Calcul de l'impédance complexe du circuit alimenté par le générateur \(\displaystyle{\{e(t), r\}}\).

Le circuit de bornes \(A\) et \(B\) se compose d'une bobine d'inductance \(L\) en série avec deux éléments en parallèle :
le condensateur et le conducteur ohmique.
L'admittance complexe du dipôle équivalent à une association de dipôles associés en série est égale à la somme de leurs impédances complexes :
\(\displaystyle{\begin{array}{lll}\underline Y_{RC} & = & \underline Y_R+\underline Y_C\\ & = & \frac{1}{R}+jC\omega\\ & = & \frac{1+jRC\omega}{R}\Rightarrow Z_{RC}=\frac{R}{1+(RC\omega)}\end{array}}\)
L'impédance complexe de dipôles associés en série est égale à la somme de leurs impédances complexes :
\(\displaystyle{\begin{array}{lll}\underline Z_{AB}&=&\underline Z_L+\underline Z_{RC}\\ & = & jL\omega+\frac{R+jL\omega}{1+jRC\omega}\\ & = & \frac{R(1-LC\omega^2)+jL\omega}{1+jRC\omega} \end{array}}\)
L'adaptation entre le générateur et sa charge est réalisée si leurs impédances complexes sont des complexes conjugués :
comme \(r\) est un réel, \(\displaystyle{\underline Z_{AB}=r=\frac{R(1-LC\omega^2)+jL\omega}{1+jRC\omega}}\) ;
En identifiant les parties réelles, on obtient :
\(\displaystyle{L=\frac{\sqrt{r(R-r)}}{\omega}}\), qui permet de tirer \(\displaystyle{C=\frac{1}{R\omega}\sqrt{\frac{R-r}{r}}}\) , solutions qui ne sont acceptables que si\(r < R\)
Les deux méthodes conduisent bien à la même solution.
b. \(( r > R)\)
1 ] Calcul de l'impédance interne complexe du générateur Thévenin alimentant \(R\).

Si on ne conserve que les éléments passifs de ce circuit pour pouvoir calculer l'impédance interne complexe du générateur de Thévenin alimentant \(R\), on obtient :

Ce circuit est analogue au cicuit du \(2\). de la question précédente, dans lequel \(R\) est remplacé par \(r\).
En échangeant \(r\) et \(R\) dans la solution, on obtient :
\(\displaystyle{L=\frac{\sqrt{R(r-R)}}{\omega}}\); \(\displaystyle{C=\frac{1}{r\omega}\sqrt{\frac{r-R}{R}}}\) , solutions qui ne sont acceptables que si \(r > R\) .
2 ] Calcul de l'impédance complexe du circuit alimenté par le générateur \(\displaystyle{\{e(t), r\}}\)

Ce circuit est analogue au circuit du 1. de la question précédente, dans lequel \(R\) est remplacé par \(r\).
En échangeant \(r\) et \(R\) dans la solution, on obtient encore : \(\displaystyle{L=\frac{\sqrt{R(r-R)}}{\omega}}\);
\(\displaystyle{C=\frac{1}{r\omega}\sqrt{\frac{r-R}{R}}}\)