Autres exemples de réponses à des excitations en force harmonique
Les réponses \(x(t)\) sont tracées ci-dessous pour deux oscillateurs ayant des paramètres \(\lambda\) et \(\omega_0\) différents, correspondants respectivement à des discriminants réduits \(\Delta' > 0\) et \(\Delta' < 0\), la pulsation de l'excitation \((\Omega = 3 \mathrm{ rad.s}^{-1})\) et les conditions initiales \((x (t = 0) = 1, x'(t = 0) = 0)\) étant les mêmes.
\(\Delta' > 0 : ~~\omega_0 = 1 \mathrm{ rad.s}^{-1}, \lambda = 5 \mathrm{ rad.s}^{-1}\)

\(\Delta' < 0 : ~~\omega_0 = 1 \mathrm{ rad.s}^{-1}, \lambda =0,01 \mathrm{ rad.s}^{-1}\)
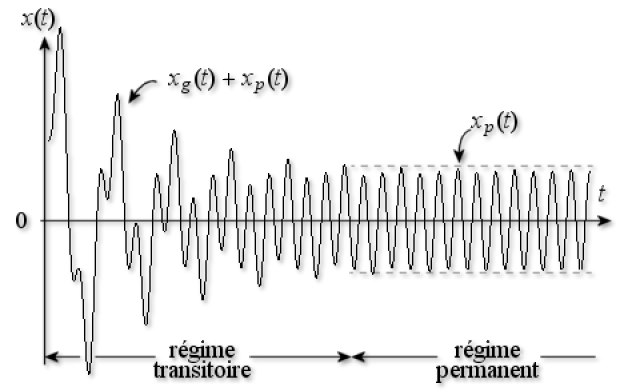
Commentaires dans le cas de l'excitation harmonique :
en régime transitoire forcé : les oscillations, de forme compliquée, sont amorties, \(x(t)\) décroît en fonction du temps.
en régime permanent : tout se passe comme si les oscillations n'étaient plus amorties, elles sont sinusoïdales pures d'amplitude constante \(x_{pm}\) et de pulsation \(\Omega\) :
La réponse de l'oscillateur forcé amorti est alors équivalente à celle d'un oscillateur harmonique de pulsation propre égale à la pulsation de l'excitation soit \(\Omega\).
L'excitateur fournit à l'oscillateur, à chaque période, une quantité d'énergie qui compense exactement l'énergie dissipée par celui-ci.