Etude de la phase des oscillations forcées en régime permanent en fonction de la pulsation de l'excitation
Rappelons que le terme \(\Phi_p\) représente le déphasage de la réponse de l'oscillateur par rapport à l'excitation.
La relation
\(\tan \Phi_p = \frac{- 2 ~\lambda ~\Omega}{\omega_0^2 - \Omega^2}\)
montre que l'oscillateur est toujours en retard de phase par rapport à l'excitation et ce retard augmente lorsque la pulsation de l'excitation augmente :
l'oscillateur et l'excitateur sont en phase pour \(\Omega = 0\) et en opposition de phase pour \(\Omega \to +\infty\)
l'oscillateur est en quadrature retard par rapport à l'excitateur à la résonance.
La figure ci-dessous représente les graphes des fonctions \(\Phi_p(\Omega)\) correspondant à des oscillateurs différents, de même pulsation propre \(\omega_0 = 1 \mathrm{ rad.s}^{-1}\) mais de coefficient d'amortissement \(\lambda\) décroissant de \(5\) à \(0,01 \mathrm{ rad.s}^{-1}\)
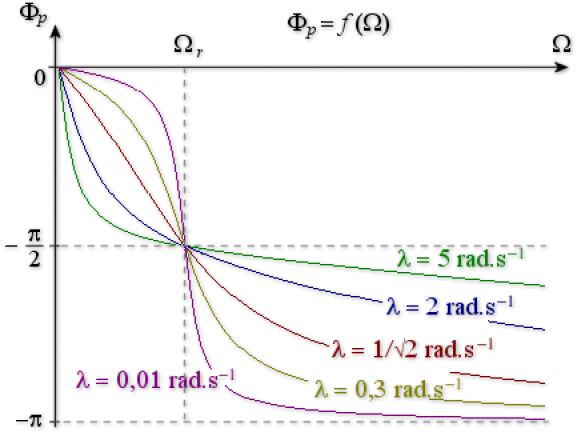
Plus le coefficient d'amortissement est faible, plus la rotation de phase autour de \(\Omega_r\) est marquée, c'est-à-dire la valeur de \(\Phi_p\) varie rapidement de \(0\) à \(-\pi\) lorsque la valeur de la pulsation de l'excitation \(\Omega\) varie de \(\Omega_r - \varepsilon\) à \(\Omega_r + \varepsilon\) (\(\varepsilon\) étant une quantité petite).
Cas de l'amortissement très faible :
Dans ce cas \(\lambda \ll \omega_0\) et \(\Omega_R \approx \omega_0\), l'oscillateur passe instantanément de l'accord à l'opposition de phase quand la pulsation franchit la valeur de la résonance.