Théorème de comparaison
Le théorème suivant montre la propriété dite de prolongement des inégalités : il exprime en effet que si deux suites convergentes sont comparables leurs limites vérifient la même inégalité.
Théorème :
Soient \((u_n)\) et \((v_n)\) deux suites réelles vérifiant
\(\displaystyle{(\forall n\in\mathbb N)\quad u_n\leq v_n}\)
\(\displaystyle{\lim_{n\to\infty}u_n=l_1}\) et \(\displaystyle{\lim_{n\to\infty}v_n=l_2}\)
on a alors \(\displaystyle{l_1\leq l_2}\).
Preuve :
Démonstration par l'absurde:
on suppose \(\displaystyle{l_2<l_1}\).
On choisit \(\displaystyle{0<\epsilon<\frac{l_1-l_2}{2}}\), ainsi les intervalles \(\displaystyle{]l_1-\epsilon,l_1+\epsilon[}\) et \(\displaystyle{]l_2-\epsilon,l_2+\epsilon[}\) sont disjoints.
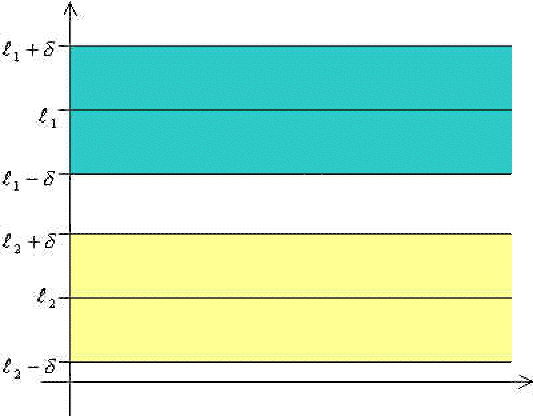
Les conditions \(\displaystyle{\lim_{n\to+\infty}u_n=l_1}\) et \(\displaystyle{\lim_{n\to+\infty}u_n=l_2}\) entraînent :
\(\displaystyle{\exists N_1,\forall n\in\mathbb N\quad(n\geq N_1\Rightarrow u_n\in]l_1-\epsilon,l_1+\epsilon[)}\)
\(\displaystyle{\exists N_2,\forall n\in\mathbb N\quad(n\geq N_2\Rightarrow v_n\in]l_2-\epsilon,l_2+\epsilon[)}\)
On pose \(\displaystyle{N=\textrm{max}(N_1,N_2)}\) alors \(n\geq N\) entraîne \(v_n < u_n\) d'où la contradiction.
Remarque :
Il suffit que les inégalités 1. soient vérifiées à partir d'un certain rang.
Si, dans la condition 1. on remplace l'inégalité large par une inégalité stricte la conclusion \(\displaystyle{l_1\le l_2}\) reste la même (inégalité large).
Par exemple les suites \(\displaystyle{\left(\frac{1}{2n}\right)_{n\geq 1}}\) et \(\displaystyle{\left(\frac{1}{n}\right)_{n\geq 1}}\) vérifient \(\displaystyle{(\forall n\in\mathbb N^*)}\) \(\displaystyle{\frac{1}{2n}<\frac{1}{n}}\) or on a \(\displaystyle{\lim_{n\to+\infty}\frac{1}{2n}=\lim_{n\to+\infty}\frac{1}{n}=0}\)
Dans le cas de suites tendant vers \(+\infty\) ou \(-\infty\) , si la condition 1. est vérifiée on ne peut conclure que dans les cas suivants :
2'. si la suite \((u_n)\) tend vers \(+\infty\) alors la suite \((v_n)\) tend vers \(+\infty\)
2". si la suite \((v_n)\) tend vers \(-\infty\) alors la suite \((u_n)\) tend vers \(-\infty\).
Il est inutile d'insister sur l'intérêt du théorème suivant tant son usage est fréquent ! Ses dénominations (théorème sandwich ou théorème des gendarmes) résument bien la situation.
Théorème :
Soient \((u_n)\), \((v_n)\) et \((w_n)\) trois suites réelles vérifiant :
\((\forall n \in \mathbb N)\) \(u_n\le v_n\le w_n\),
\(\displaystyle{\lim_{n\to\infty}u_n=\lim_{n\to\infty}w_n=l} \);
alors la suite \((v_n)\) converge et a pour limite \(l\).
Preuve :
L'écriture de la convergence des suites \(u_n\) et \(w_n\) fait apparaître des rangs \(N_1\) et \(N_2\). On considère \(N=\textrm{ max }(N_1,N_2)\) .
En effet :
La condition 1. entraîne, pour tout \(n\in\mathbb N\):
\(\displaystyle{u_n-l\leq v_n-l\leq w_n-l}\).
La condition 2. entraine, pour tout \(\epsilon>0\):
\(\displaystyle{\exists N_1,\forall n\in\mathbb N\quad(n\geq N_1\Rightarrow\vert u_n-l\vert<\epsilon)}\)
\(\displaystyle{\exists N_2,\forall n\in\mathbb N\quad(n\geq N_2\Rightarrow\vert w_n-l\vert<\epsilon)}\)
D'où, en posant \(\displaystyle{N=\textrm{ max }(N_1,N_2)}\), l'inégalité \(n \geq N\) entraîne
\(\displaystyle{l-\epsilon< u_n\leq v_n\leq w_n< l+\epsilon}\)