Exercice 2
Durée : 5 mn
Note maximale : 5
Question
On considère trois fonctions numériques \(f\), \(g\) et \(h\) définies sur un intervalle ouvert \(I\) contenant 0 ; on suppose que l'on a : \(\forall x\in I~f(x)\le g(x)\le h(x)\)
les assertions suivantes sont-elles vraies ou fausses :
Si \(f\) et \(h\) sont continues en 0, alors \(g\) est continue en 0,
Si \(f\) et \(h\) sont bornées sur \(I\) , alors g est bornée sur \(I\),
L'égalité \(\displaystyle{\lim_{x\rightarrow0}(h-f)=0}\) entraîne que \(g\) a une limite en 0 ?
Solution
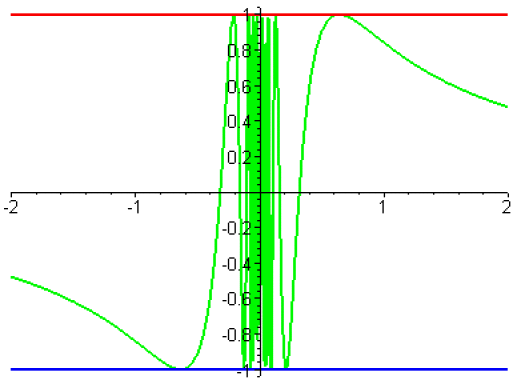
1. Faux : on prend le contrexemple suivant : les fonctions \(f\) et \(h\) sont les fonctions constantes, égales respectivement à
\(-1\) et \(1\) et \(g\) est la fonction \(\displaystyle{x\mapsto\sin~\left(\frac{1}{x}\right)}\) prolongée en 0 par un réel \(m\) vérifiant : \(-1\le m\le1\).
[2 points]
2. Vrai : les fonctions \(f\) et \(g\) étant bornées sur \(I\) on a :
\(\forall x\in I,~|f(x)|\le M_1\) et \(|h(x)|\le M_2\) d'où \(\forall x\in I,~|g(x)|\le\max(M_1,M_2)\)
[1 point]
3. Faux : Il suffit de prendre le contre-exemple très simple suivant : les trois fonctions sont égales à la fonction \(\displaystyle{x\mapsto\sin~\left(\frac{1}{x}\right)}\) prolongée en \(0\) par un réel \(m\) vérifiant : \(-1\le m\le1\).
[2 points]