Équation cartésienne d'un plan défini par un point et deux vecteurs directeurs
Partie
Question
On se place dans le plan \(\epsilon_3\) muni d'un repère \((O,\vec{i},\vec{j})\).
Vérifier que les vecteurs \(\vec{u}\) de coordonnées \((0,1,-1)\) et \(\vec{v}\) de coordonnées \((1,2,3)\) sont linéairement indépendants. Trouver une équation cartésienne du plan \(P\) passant par le point \(M_0\) de coordonnées \((1,-1,3)\) et de vecteurs directeurs \(\vec{u}\), \(\vec{v}\).
Aide simple
Les points \(A\) et \(B\) ayant pour coordonnées respectives \((x_A,y_A,z_A)\) et \((x_B,y_B,z_B)\), le triplet des coordonnées du vecteur \(\overrightarrow{AB}\) est \((x_B-x_A,y_B-y_A,z_B-z_A)\).
Aide méthodologique
Un point \(M\) de coordonnées \((x,y,z)\) appartient au plan \(P\) passant par le point \(M_0\) de coordonnées \((1,-1,3)\) et de vecteurs directeurs \(\vec{u}\), \(\vec{v}\), si et seulement si la famille \(\left\{\overrightarrow{M_0M},\vec{u},\vec{v}\right\}\)est liée.
Aide à la lecture
On se place ici dans l'espace de la géométrie usuelle, il est muni d'un repère \((O,\vec{i},\vec{j},\vec{k})\) et un triplet \((x,y,z)\) représente les coordonnées d'un point \(M\) ou d'un vecteur \(\vec{w}\) dont un représentant est \(\overrightarrow{OM}\).
Solution détaillée
Les vecteurs \(\vec{u}\), \(\vec{v}\) sont linéairement indépendants car on peut extraire un mineur d'ordre 2 non nul de la matrice de leurs coordonnées, par exemple \(\left|\begin{array}{cc}0&1\\1&2\end{array}\right|=-1\)
Un point \(M\) de coordonnées \((x,y,z)\) appartient au plan \(P\) passant par le point \(M_0\) et de vecteurs directeurs \(\vec{u}\), \(\vec{v}\) , si et seulement si le vecteur \(\overrightarrow{M_0M}\) est combinaison linéaire des vecteurs \(\vec{u}\) et \(\vec{v}\) ; ces derniers étant linéairement indépendants ceci est équivalent à : " la famille \(\left\{\overrightarrow{M_0M},\vec{u},\vec{v}\right\}\) est liée ".
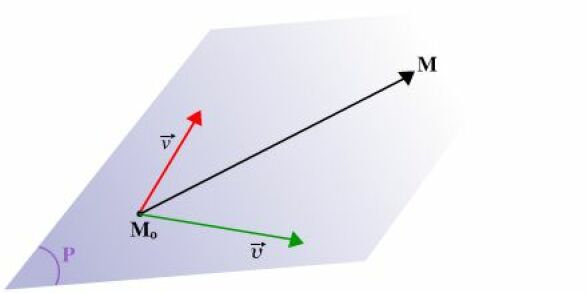
Une condition nécessaire et suffisante pour que le point \(M\) appartienne au plan \(P\) est donc que le déterminant de ces trois vecteurs soit nul.
Les coordonnées du vecteur \(\overrightarrow{M_0M}\) sont \((x-1,y+1,z-3)\).
On obtient donc la condition :
\(\left|\begin{array}{ccc}x-1&0&1\\y+1&1&2\\z-3&-1&3\end{array}\right|=0\)
D'où, en développant suivant la première colonne :
\(5(x-1)-(y+1)-(z-3)=0\)
Une équation cartésienne du plan \(P\) est donc :
\(5x-y-z-3=0\)