Langage des ensembles

Inclusion d'ensembles

On dit qu'un ensemble \(F\) est inclus dans un ensemble \(E,\) si tout élément de \(F\) appartient à \(E.\)

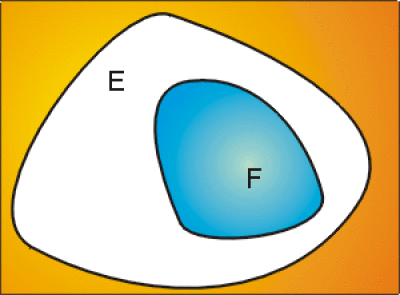
\(\begin{array}{l l} F \subset E &F \textrm{ est inclus dans l'ensemble } E\\ F \subset E & F \textrm{ est contenu dans l'ensemble } E\\F\subset E &F  \textrm{ est un sous-ensemble de l'ensemble } E\\F\subset E &F \textrm{ est une partie de l'ensemble } E\\F\not\subset E &F \textrm{ est la négation de }F \subset E\\F\not\subset E &F \textrm{ n'est pas inclus dans l'ensemble } E\\F\not\subset E& F \textrm{ signifie "il existe au moins un élément de } F  \textrm{ n'appartenant pas à } E"\end{array}\)

L'inclusion est une inclusion large

D'après la définition précédente, tout ensemble \(E\) est inclus dans lui même.

\(E\subset E\)

Inclusion stricte

Lorsque le sous-ensemble \(F\) est strictement inclus dans l'ensemble \(E,\) on dit que \(F\) est un sous-ensemble propre de \(E.\) On doit alors le préciser par la conjonction des deux propriétés:

\(F\subset E~ et~ F \neq E\)

Ensemble vide et inclusion

L'ensemble vide est contenu dans tout ensemble \(E.\)

\(\emptyset \subset E\)

Un ensemble \(E\) non vide a donc toujours au moins deux sous-ensembles, l'ensemble vide et lui même. Par contre, l'ensemble \(\emptyset\) a un seul sous-ensemble, lui-même.

Exemples d'inclusion d'ensembles

\(\mathbb N \subset \mathbb Z,\) \(\mathbb Z \subset \mathbb D,\) \(\mathbb D \subset \mathbb Q,\) \(\mathbb Q \subset \mathbb R,\) \(\mathbb R \subset \mathbb C\)

Soit l'ensemble \(E = \{a, b, c\}.\) Ses sous-ensembles sont les ensembles :

\(\emptyset, \{a\}, \{b\}, \{c\}, \{a, b\}, \{a, c\}, \{b, c\},\{a, b, c\}\)

Transitivité de l'inclusion :

\(A,~B, ~C\) étant trois ensembles, si le premier ensemble \(A\) est contenu dans le second \(B,\) si le deuxième ensemble \(B\) est contenu dans le troisième \(C,\) alors le premier ensemble \(A\) est contenu dans le troisième \(C\) ; on dit que l'inclusion est transitive ; cette propriété s'énonce:

Si \((A\subset B~et~ B\subset C),\) alors \(A\subset C\)

et s'écrit en langage formalisé où \(\Rightarrow\)se lit "implique" et sera revu dans la suite :

\((A\subset B~et~ B\subset C)\Rightarrow A\subset C\)

Justification

Soit \(x\) un élément de \(A,\) d'après l'hypothèse \(A\subset B,\) on peut affirmer que \(x\) est élément de \(B.\) D'après l'hypothèse \(B\subset C,\) on peut affirmer que \(x\) est élément de \(C.\) On a donc montré que tout élément de \(A\) est élément de \(C\) et donc que \(A\) est inclus dans \(C.\)

Abus d'écriture

On peut écrire une série d'inclusions qui met en évidence la transitivité de l'inclusion :

\(\mathbb N \subset \mathbb Z\subset \mathbb D\subset \mathbb Q\subset \mathbb R\subset \mathbb C\)

Égalité d'ensembles :

Deux ensembles \(E\) et \(F\) sont égaux s'ils ont exactement les mêmes éléments. Cela se traduit par deux inclusions simultanées.

\(E= F \Leftrightarrow (F\subset E~et~E\subset F)\)