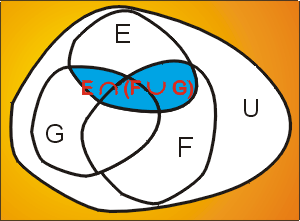
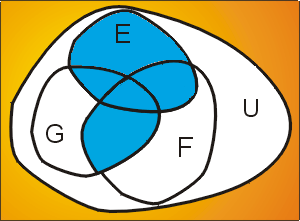
Propriétés de distributivité
Démonstration :
Première indication
Pour montrer une égalité d'ensemble on doit démontrer deux inclusions :
\(E\cap (F\cup G) \subset (E\cap F)\cup (E\cap G)\)
\((E\cap F)\cup (E\cap G)\subset E\cap (F\cup G)\)
Pour montrer une inclusion d'ensembles, on regarde si on peut utiliser des propriétés connues, sinon on prend un élément du premier ensemble et on montre qu'il appartient au second.
Deuxième indication
\(E\cap (F\cup G) \subset (E\cap F)\cup (E\cap G)\)
Pour montrer cette inclusion prendre un élément de \(E\cap (F\cup G)\) et montrer qu'il appartient à \((E\cap F)\cup (E\cap G).\)
On commence donc par «soit \(x\in E\cap(F\cup G)\dots\)»
\((E\cap F)\cup (E\cap G)\subset E\cap (F\cup G)\)
Pour montrer cette inclusion, utiliser des propriétés connues de l'intersection et de la réunion d'ensembles.
Démonstration détaillée
Première inclusion
\(E\cap (F\cup G) \subset (E\cap F)\cup (E\cap G)\)
Soit \(x\) un élément de \(E\cap (F\cup G).\) L'élément \(x\) appartient à la fois à \(E\) et à \(F\cup G,\) donc\( x\in F\) ou \(x\in G.\) Nous trouvons deux cas possibles :
Premier cas : \(x\) appartient à \(F,\) donc à \(E\cap F.\) Comme \(E\cap F\) est un sous-ensemble de \((E\cap F)\cup (E\cap G),\) cela montre que \(x\) est élément de \((E\cap F)\cup (E\cap G),\) ce qu'il fallait démontrer.
Deuxième cas : \(x\) appartient à \(G,\) donc à \(E\cap G,\) sous-ensemble de \((E\cap F)\cup (E\cap G),\) cela montre que \(x\) est élément de \((E\cap F)\cup (E\cap G),\) ce qu'il fallait démontrer.
Conclusion : Par conséquent on a montré que tout élément de \(E\cap (F\cup G)\) est élément de \((E\cap F)\cup (E\cap G),\) et donc l'inclusion cherchée.
Deuxième inclusion
\((E\cap F)\cup (E\cap G)\subset E\cap (F\cup G)\)
Pour montrer cette inclusion, on va utiliser la propriété connue de la réunion de deux ensembles (qui est le plus petit ensemble contenu dans les deux).
\(E\cap F\subset E~et~ E\cap G\subset E\)
donc : \((E\cap F)\cup (E\cap G)\subset E\)
\(E\cap F\subset F\subset F\cup G~ et~ E\cap G\subset G\subset F\cup G\) donc,
\((E\cap F)\cup (E\cap G)\subset F\cup G\)
On utilise maintenant la propriété connue de l'intersection de deux ensembles (qui est le plus grand ensemble contenu dans les deux). Puisque \((E\cap F)\cup (E\cap G)\) est un sous-ensemble à la fois de \(E\) et de \(F\cup G,\) la conjonction des deux inclusions montrées précédemment entraîne l'inclusion cherchée :
\((E\cap F)\cup (E\cap G)\subset E\cap(F\cup G).\)
La réunion est distributive par rapport à l'[3] intersection[3]
Cela résulte de la distributivité de la disjonction par rapport à la conjonction. Démontrer cette propriété en utilisant les mêmes méthodes que dans la démonstration précédente.
\(E\cup (F\cap G) = (E\cup F)\cap (E\cup G)\)