Projecteurs
Soit \(E\) un espace vectoriel de type fini.
Définition :
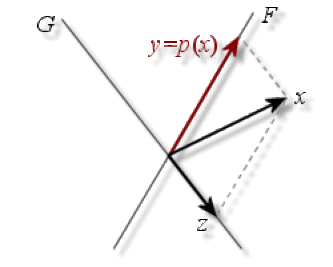
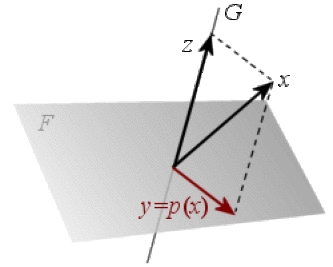
Soient \(F\) et \(G\) deux sous-espaces vectoriels supplémentaires de \(E\), donc tels que \(E=F\oplus G\). Pour tout \(x\) de \(E\) il existe un unique couple \((y,z)\) appartenant à \(F\times G\) tel que \(x=y+z\).
L'application qui à \(x\) associe sa composante \(y\) sur \(F\) est le projecteur sur le sous-espace \(F\) parallèlement à \(G\).
\(\begin{array}{ccccccc}p :E&=&F&\oplus&G&\to&E\\x&=&y&+&z&\mapsto&y\end{array}\)
Projecteur dans \(\mathbb R^2\)
Projecteur dans \(\mathbb R^3\)
Les propriétés suivantes sont immédiates.
Proposition : Propriétés vectorielles d'un projecteur
Un projecteur est une application linéaire.
Si \(E=F\oplus G\) et si \(p\) est le projecteur sur le sous-espace vectoriel \(F\) parallèlement à \(G\), alors :
\(\begin{array}{cccccc}\textrm{Im}p&=&F\\\textrm{Ker}p&=&G\end{array}\)
Remarque :
\(q=Id_E-p\) est le projecteur sur \(G\) parallèlement à \(F\).
On en déduit immédiatement les corollaires suivants :
Corollaire :
Si \(E=F\oplus G\) et si \(p\) est le projecteur sur le sous-espace vectoriel \(F\) parallèlement à \(G\), alors :
\(E=\textrm{Ker}p\oplus\textrm{Im}p\)
Corollaire :
Si \(E=F\oplus G\) et si \(p\) est le projecteur sur le sous-espace vectoriel \(F\) parallèlement à \(G\), alors :
\(\begin{array}{cccccc}\forall x&\in&F,p(x)&=&x\\\forall x&\in&G,p(x)&=&0\end{array}\)
En effet si \(x\) appartient à \(F\), l'écriture de \(x\) comme somme d'un élément de \(F\) et d'un élément de \(G\) est \(x=x+0\) et par conséquent \(p(x)=x\).
De même si \(x\) appartient à \(G\), l'écriture de \(x\) comme somme d'un élément de \(F\) et d'un élément de \(G\) est \(x=0+x\) et par conséquent \(p(x)=0\).
Une conséquence de ces propriétés est la stabilité par \(p\) des sous-espaces \(F\) et \(G\).
Nous allons donner une caractérisation d'un projecteur.
Théorème : Caractérisation d'un projecteur
Si \(p\) est un projecteur, on a : \(p^2=p\).
Réciproquement si \(p\) est un endomorphisme de \(E\) tel que \(p^2=p\), alors \(p\) est le projecteur sur parallèlement à \(\textrm{Ker }p\).
Preuve : Preuve du 1.
si \(x=y+z\) avec \(y\) élément de \(F\) et \(z\) élément de \(G\), on a :
\(p(x)=y\), d'où \(p^2(x)=p(y)=y=p(x)\) puisque \(y\) appartient à \(F\).
Preuve : Preuve du 2.
si \(p\) est un endomorphisme de \(E\) tel que \(p^2=p\), alors on a \(E=\textrm{ Ker }p\oplus\textrm{ Im }p\). En effet, soit \(x\) un élément de \(\textrm{Ker }p\;\cap\textrm{ Im }p\). Alors on a les deux propriétés :
\(p(x)=0\)
\(\exists t\in E,x=p(t)\)
Comme \(p^2=p\), il vient \(p^2(t)=p(t)\) et donc \(p(x)=x\). D'où \(x=0\). Le théorème du rang permet de conclure, grâce à un argument de dimension, que \(E=\textrm{Ker }p\;\oplus\textrm{ Im }p\), d'où le résultat.
Proposition : Matrice associée à un projecteur
Soient \(F\) et \(G\) deux sous-espaces vectoriels de \(E\), non réduits au vecteur nul et supplémentaires \((E=F\oplus G)\).
Soient \(B_F\) et \(B_G\) des bases de \(F\) et \(G\) respectivement. Soit \(p\) le projecteur sur \(F\) parallèlement à \(G\).
La matrice de \(p\) dans la base déterminée par la réunion des vecteurs de \(B_F\) et \(B_G\) est égale à \(\left(\begin{array}{cc}I_r&0_{n-r}\\0_{r}&0_{n-r}\end{array}\right)\) où \(r\) est la dimension de \(F\).
La matrice \(I_r\) est la matrice unité d'ordre \(r\). La matrice \(0_{n-r}\) est la matrice carrée d'ordre \(n-r\) dont tous les coefficients sont nuls.
On peut interpréter ce résultat dans le langage de la théorie de la diagonalisation. En effet ce résultat signifie qu'un projecteur est diagonalisable, que ses valeurs propres sont \(1\) et \(0\) et enfin que le sous-espace propre associé à la valeur propre \(0\) est \(G\) et celui associé à la valeur propre \(1\) est \(F\).
Remarque :
Sauf dans le cas où \(n=2\), cela donne un exemple d'endomorphisme diagonalisable ayant un nombre de valeurs propres distinctes strictement inférieur à la dimension \(n\) de l'espace considéré.