Affinités
Soit \(E\) un espace vectoriel de type fini.
Définition :
Soient \(F\) et \(G\) deux sous-espaces vectoriels de \(E\), non réduits au vecteur nul et supplémentaires, donc tels que \(E=F\oplus G\). Soit \(\lambda\) un élément de \(\mathbf K\).
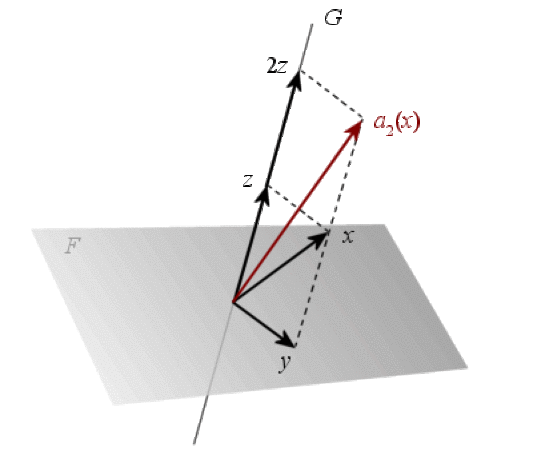
Pour tout \(x\) de \(E\), il existe un unique couple \((y,z)\) appartenant à \(F\times G\) tel que \(x=y+z\). L'application :
\(\begin{array}{cccccc}a_\lambda :E&=&F\oplus G&\to&E\\x&=&y+z&\mapsto&y+\lambda z\end{array}\)
est l'affinité de rapport \(\lambda\), par rapport au sous-espace \(F\) et parallèlement à \(G\).
Affinité de rapport \(2\) dans \(\mathbb R^3\)
Proposition : Propriétés vectorielles
Une affinité est une application linéaire.
Si \(a_\lambda\) est l'affinité de rapport \(\lambda\), par rapport au sous-espace \(F\) et parallèlement à \(G\), alors les sous espaces \(F\) et \(G\) sont stables par \(a_\lambda\). La restriction de \(a_\lambda\) à \(F\) est l'identité ; la restriction de \(a_\lambda\) à \(G\) est l'homothétie de rapport \(\lambda\). On a :
\(\begin{array}{cccccc}\forall x\in F,&a_\lambda(x)=x\\\forall x\in G,&a_\lambda(x)=\lambda x\end{array}\)
Remarque :
La symétrie par rapport au sous-espace \(F\) et parallèlement à \(G\) est l'affinité de rapport \(-1\), par rapport au sous-espace \(F\) et parallèlement à \(G\). La projection par rapport au sous-espace \(F\) et parallèlement à \(G\) est l'affinité de rapport \(0\), par rapport au sous-espace \(F\) et parallèlement à \(G\).
Enfin on a le résultat suivant sur la matrice associée à une symétrie dans une base bien choisie.
Proposition : Matrice associée à une affinité
Soient \(F\) et \(G\) deux sous-espaces supplémentaires de \(E\), non réduits au vecteur nul. Soient \(B_F\) et \(B_G\) des bases de \(F\) et \(G\) respectivement. Soit \(a_\lambda\) l'affinité de rapport \(\lambda\), par rapport au sous-espace \(F\), parallèlement à \(G\).
Sa matrice dans la base déterminée par la réunion des vecteurs de \(B_F\) et \(B_G\) est égale à \(M=\left(\begin{array}{cc}I_r&0\\0&\lambda I_q\end{array}\right)\) où \(r\) est la dimension de \(F\) et \(q\) celle de \(G\).
On peut interpréter ce résultat dans le langage de la théorie de la diagonalisation. En effet ce résultat signifie que l'affinité de rapport \(\lambda\), par rapport à \(F\) et parallèlement à \(G\) est diagonalisable, que ses valeurs propres sont \(1\) et \(\lambda\) et enfin que le sous-espace propre associé à la valeur propre \(\lambda\) est \(G\) et celui associé à la valeur propre \(1\) est \(F\).
On en déduit la caractérisation suivante :
Théorème : Caractérisation d'une affinité
Soit \(E\) un espace vectoriel de type finie
Si \(a_\lambda\) est une affinité de rapport \(\lambda\), on a :
\((a_\lambda-Id_E)\bigcirc(a_\lambda-\lambda Id_E)={a_\lambda}^2-(1+\lambda)a_\lambda+\lambda Id_E=0\)
Réciproquement soit \(\lambda\) un scalaire différent de \(1\) et \(a\) un endomorphisme de \(E\) tel que \(a^2-(1+\lambda)a+\lambda Id_E=0\), alors \(a\) est l'affinité de rapport \(\lambda\) par rapport à \(F=\left\{x\in E,a(x)=x\right\}\) parallèlement à \(G=\left\{x\in E,a(x)=\lambda x\right\}\).
Preuve : Preuve de la propriété 1.
La propriété 1. peut être facilement vérifiée grâce au calcul matriciel. En effet la matrice associée à l'endomorphisme \((a_\lambda-Id_E)\bigcirc(a_\lambda-\lambda Id_E)\) par rapport à la base déterminée par la réunion des vecteurs de \(B_F\) et \(B_G\) est égale à \((M-I_n)(M-\lambda I_n)\). Alors
\((M-I_n)(M-\lambda I_n)=\left(\begin{array}{cc}0_r&0\\0&(\lambda-1)I_q\end{array}\right)\left(\begin{array}{cc}(1-\lambda)I_r&0\\0&0_q\end{array}\right)=0\).
Preuve : Preuve de la propriété 2.
Pour justifier la propriété 2. on montre que \(F\) et \(G\) sont des sous-espaces vectoriels de \(E\) et que \(E\) est somme directe de \(F\) et \(G\). Pour cela on suit le plan suivant :
Comme \(F=\textrm{ ker }(a-Id_E)\) et \(G=\textrm{ ker }(a-\lambda Id_E)\), \(F\) et \(G\) sont des sous-espaces vectoriels de \(E\).
On vérifie que \(F\cap G=\left\{0\right\}\) (l'hypothèse utile est ici \(\lambda\neq1\))
On montre que tout élément de \(E\) s'écrit comme somme d'un élément de \(F\) et d'un élément de \(G\).
Pour cela on utilise la méthode classique : on suppose le problème résolu et on trouve la seule décomposition possible d'un vecteur de \(E\) (là encore l'hypothèse essentielle est \(\lambda\neq1\)). Ensuite on vérifie que c'est une solution du problème et c'est à ce niveau qu'est utilisé l'hypothèse \(a^2-(1+\lambda)a+\lambda Id_E=0\).
Cela permet de caractériser \(a\).
Complément : Preuve complète de la propriété 2.
Première étape :
\(F\cap G=\{0\}\).
Soit donc un élément \(x\) de \(F\cap G\). Il vérifie les deux égalités :
\(\begin{array}{cccccc}a(x)&=&x\\a(x)&=&\lambda x\end{array}\)
Comme \(\lambda\) est différent de \(1\), elles impliquent que \(x=0\).
Deuxième étape :
tout élément de \(E\) s'écrit comme somme d'un élément de \(F\) et d'un élément de \(G\).
Supposons le problème résolu. Cela signifie qu'il existe un élément \(x_F\) de \(F\) et un élément \(x_G\) de \(G\) tels que \(x=x_F+x_G\). Alors
\(a(x)=a(x_F)+a(x_G)=x_F+\lambda x_G\).
Des égalités \(x=x_F+x_G\) et \(a(x)=x_F+\lambda x_G\) et de l'hypothèse \(\lambda\neq1\), on déduit immédiatement que :
\(\displaystyle{x_F=\frac{1}{1-\lambda}(a(x)-\lambda x)}\), \(\displaystyle{x_G=\frac{1}{\lambda-1}(a(x)-x)}\)
Pour terminer la démonstration, il faut démontrer que ces valeurs conviennent c'est-à-dire que leur somme est égale à \(x\), que \(\displaystyle{\frac{1}{1-\lambda}(a(x)-\lambda x)}\) appartient à \(F\) et que \(\displaystyle{\frac{1}{\lambda-1}(a(x)-\lambda x)}\) appartient à \(G\).
On a :
\(\displaystyle{\begin{array}{cccccc}\frac{1}{1-\lambda}(a(x)-\lambda x)+\frac{1}{\lambda-1}(a(x)-x)&=&\frac{1}{1-\lambda}\left[(a(x)-\lambda x)-(a(x)-x)\right]\\&=&\frac{1}{1-\lambda}(-\lambda+1)x\\&=&x\end{array}}\)
Calculons \(\displaystyle{a\left(\frac{1}{1-\lambda}(a(x)-\lambda x)\right)}\).
On obtient : \(\displaystyle{a\left(\frac{1}{1-\lambda}(a(x)-\lambda x)\right)=\frac{1}{1-\lambda}\left[a^2(x)-\lambda a(x)\right]}\).
Or d'après l'hypothèse faite, \(a^2=(1+\lambda)a-\lambda Id_E\).
Donc \(\displaystyle{\frac{1}{1-\lambda}\left[a^2(x)-\lambda a(x)\right]=\frac{1}{1-\lambda}\left[a(x)-\lambda x\right]}\).
Donc \(\displaystyle{a\left(\frac{1}{1-\lambda}(a(x)-\lambda x)\right)=\frac{1}{1-\lambda}(a(x)-\lambda x)}\).
De même \(\displaystyle{a\left(\frac{1}{\lambda-1}(a(x)-x)\right)=\frac{1}{\lambda-1}\left[a^2(x)-a(x)\right]}\).
Comme \(a^2=(1+\lambda)a-\lambda Id_E\), il vient \(\displaystyle{\frac{1}{\lambda-1}\left[a^2(x)-a(x)\right]=\frac{\lambda}{\lambda-1}\left[a(x)-x\right]}\).
Par conséquent \(\displaystyle{a\left(\frac{1}{\lambda-1}(a(x)-x)\right)=\lambda\left(\frac{1}{\lambda-1}(a(x)-x)\right)}\).
Ceci achève la démonstration.
Remarque :
Si \(\lambda=1\), une application linéaire vérifiant \(a^2-(1+\lambda)a+\lambda Id_E=0\) (c'est-à-dire \((a-Id_E)^2=0\)) n'est pas nécessairement égale à une affinité de rapport \(1\) (qui est l'identité). Par exemple l'endomorphisme de \(\mathbb R^2\) dont la matrice dans la base canonique est égale à \(\left(\begin{array}{cc}1&1\\0&1\end{array}\right)\) est bien tel que \((a-Id_{\mathbb R^2})^2=0\) et n'est pas égal à l'identité.