Théorèmes de comparaison
Le théorème de comparaison, qui repose sur les propriétés des suites croissantes, et surtout son corollaire (second théorème de comparaison) jouent un rôle fondamental dans l'étude des séries.
Théorème : Premier théorème de comparaison
Soient \((u_n)\) et \((v_n)\) deux suites de nombres positifs vérifiant : \(\forall n \in \mathbb N\), \(u_n\leq v_n\).
- Si la série de terme général \(v_n\) est convergente, la série de terme général \(u_n\) est convergente. On a alors : \(\displaystyle{\sum_{n=0}^{+\infty}}u_n\leq\displaystyle{\sum_{n=0}^{+\infty}}v_n\).
- Si la série de terme général \(u_n\) est divergente, la série de terme général \(v_n\) est divergente.
Preuve :
Elle repose sur le théorème de comparaison des suites appliqué aux suites partielles croissantes \((s_n)\) et \((t_n)\) définies par : \(s_n=\displaystyle{\sum_{k=0}^n}u_k\) et \(t_n=\displaystyle{\sum_{k=0}^n}v_k\). On a : \(\forall n\in \mathbb N, 0\leq s_n\leq t_n\).
D'où les implications :
\(\sum v_n\) convergente \(\Rightarrow (t_n)\) bornée \(\Rightarrow (s_n)\) bornée \(\Rightarrow \sum u_n\) convergente ;
on a alors, d'après le théorème de prolongement des inégalités : \(\displaystyle{\sum_{n=0}^{+\infty}}u_n\leq \displaystyle{\sum_{n=0}^{+\infty}}v_n\).
\(\sum u_n\) divergente \(\Rightarrow (s_n)\) non bornée \(\Rightarrow (t_n)\) non bornée \(\Rightarrow \sum v_n\) divergente.
Remarque : fondamentale
Le théorème, en ce qui concerne la nature des séries, reste vrai si les inégalités \(0\leq u_n\leq v_n\) sont vérifiées à partir d'un certain rang (ce n'est pas vrai pour la comparaison des sommes).
Application. Le théorème de comparaison permet de donner une autre démonstration du théorème sur la convergence des séries absolument convergentes.
Preuve :
Il s'agit de montrer que toute série \(\sum u_n\) telle que la série \(\sum |u_n|\) est convergente, est également convergente. Compte tenu des inégalités \(\textrm{Re}(u_n)\leq|u_n|\) et \(\textrm{Im}(u_n)\leq|u_n|\), il suffit de montrer cette propriété pour des séries réelles.
On considère donc une série \(\sum u_n\) à termes réels. On a, pour tout \(n\) : \(u_n^+\leq|u_n|\) et \(u_n^-\leq|u_n|\). Ainsi, si la série \(\sum |u_n|\) est convergente, il en est de même des séries \(\sum u_n^+\) et \(\sum u_n^-\), et donc de la série \(\sum u_n\).
Exemple :
On se réfère à des séries connues comme séries de comparaison.
étude de la série de terme général \(u_n=\frac{2+\sin n}{3^n}\)
On a : \(\forall n \geq 0\), \(0<u_n\leq\frac{3}{3^n}=\frac{1}{3^{n-1}}\). La série \(\sum \frac{2+\sin n}{3^n}\)est convergente.
étude de la série de terme général \(u_n=\frac{1}{\ln n+\sqrt{n}} ~(n\geq 1)\)
On a : \(\forall n\geq 1\), \(0<\ln n+\sqrt{n}\leq 2\sqrt{n}\), d'où \(\frac{1}{\ln n+\sqrt{n}}\geq\frac{1}{2\sqrt{n}}\).
La série \(\displaystyle{\sum_{n\geq 1}}\frac{1}{\sqrt{n}}\) est divergente, on en déduit que la série \(\displaystyle{\sum_{n\geq 1}}\frac{1}{\ln n+\sqrt{n}}\) est divergente.
Théorème : Second théorème de comparaison.
Soient \((u_n)\) et \((v_n)\) deux suites de nombres positifs. On suppose qu'une des conditions \(a\) ou \(b\) est vérifiée :
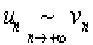
le rapport \(\frac{u_n}{v_n}\) est défini à partir d'un certain rang et admet une limite \(L\) non nulle quand n tend vers \(+\infty\).
Alors les séries \(\sum u_n\) et \(\sum v_n\) sont de même nature.
Preuve :
On étudie les deux cas en appliquant le théorème précédent.
La propriété
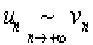signifie qu'on a \(u_n=(1+\epsilon(n))v_n\) avec \(\displaystyle{\lim_{n\rightarrow +\infty}}\epsilon(n)=0\) et donc, à partir d'un certain rang \(N\), \(\frac12 v_n<u_n<\frac32 v_n\). On applique alors le théorème précédent.Comme la limite \(L\) est non nulle, donc strictement positive compte tenu des hypothèses, on peut prendre \(\epsilon>0\) tel que \(L-\epsilon>0\).
Il existe donc un rang \(n_0\) à partir duquel \(\frac{u_n}{v_n}\) est défini et
\(\forall n\geq n_0\), \(0<L-\epsilon<\frac{u_n}{v_n}<L+\epsilon\).
Le terme général \(v_n\) est strictement positif pour tout entier \(n\geq n_0\). On a donc :
\(\forall n\geq n_0\),\(0<(L-\epsilon)v_n<u_n<(L+\epsilon)v_n\)
On applique alors le théorème précédent.
Remarque : fondamentale
Les théorèmes de comparaison concernent des séries à termes positifs (plus généralement de signe constant à partir d'un certain rang).
La condition de signe constant est indispensable. Ainsi, les séries \(\displaystyle{\sum_{n\geq 2}}\frac{(-1)^n}{\ln n}\) et \(\displaystyle{\sum_{n\geq 2}}\frac{(-1)^n}{\ln n+(-1)^n}\) vérifient
.
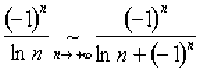Pourtant, elles ne sont pas de même nature, comme nous le verrons au paragraphe concernant le théorème des séries alternées.
Exemple :
Étude de la série de terme général \(u_n=\frac{3^n+\ln n-2^n-n^3}{\sqrt{n}+n^4+5n}~(n\geq 1)\)
On remarque que les premiers termes de cette série sont négatifs, mais on a :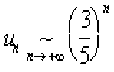 
, ce qui a pour conséquence que la série est à termes positifs à partir d'un certain rang. Elle est donc convergente par application du théorème précédent.
Les théorèmes de comparaison constituent un outil fondamental dans l'étude des séries. Il s'agit maintenant d'avoir un catalogue de séries classiques dont on connaît la nature. C'est le cas des séries géométriques ; on sait par ailleurs que la série harmonique \(\displaystyle{\sum_{n\geq 1}}\frac1n\) est divergente. Il en est donc de même, par comparaison, des séries \(\displaystyle{\sum_{n\geq 1}}\frac{1}{n^s}\) pour \(0<s\leq 1\). Dans un premier temps, les règles de d'Alembert et de Cauchy vont nous permettre de rendre plus opérationnelle la comparaison aux séries géométriques pour certains types de séries à convergence rapide. Dans un second temps, nous allons élargir le catalogue des séries de référence aux séries \(\displaystyle{\sum_{n\geq 1}}\frac{1}{n^s}\) pour \(s>1\).