Séries de Riemann. Applications
La connaissance de la nature des séries de Riemann, séries de terme général \(\frac{1}{n^s}(n\geq 1,s>0)\), jointe au théorème de comparaison, constitue le principal outil dans l'étude des séries à termes positifs et, en tenant compte de la convergence absolue, des séries en général.
Théorème :
La série de terme général est \(\frac{1}{n^s}(n\geq 1,s>0)\)
convergente si \(s > 1\),
divergente si \(s\leq 1\).
Preuve :
On utilise une comparaison entre série et intégrale.
Pour \(n\geq 1\), on pose \(u_n=\frac{1}{n^s}\) et \(v_n=\int_n^{n+1}\frac{1}{t^s}dt\).
Interprétation :
On suppose \(s > 0\), (pour \(s\leq 0\) le terme général ne tend pas vers 0 et la série est divergente). À la série \(\displaystyle{\sum_{n\geq1}}\frac{1}{n^s}\), on associe la fonction, définie sur l'intervalle \(]0+\infty[\), \(x\rightarrow\frac{1}{x^s}\), ce qui a l'avantage de donner une représentation géométrique du terme général. En considérant cette fonction sur l'intervalle \([k,k+1](k\geq 1)\), on a :
\(u_{k+1}=\frac{1}{(k+1)^s}\leq\int_k^{k+1}\frac{dt}{t^s}\leq\frac{1}{k^s}=u_k\).
D'où, en additionnant ces inégalités membre à membre \((k\in\{1,2,\ldots,n\})\), on obtient, pour \(s\neq 1\):
\(\displaystyle{\sum_{k=2}^{n+1}}\frac{1}{k^s}\leq\int_1^{n+1}\frac{dt}{t^s}\leq\displaystyle{\sum_{k=1}^n}\frac{1}{k^s}\) soit \(s_{n+1}-u_1\leq \frac{1}{1-s}\left(\frac{1}{(n+1)^{s-1}}-1\right)\leq s_n\).
Pour \(s = 1\), on a : \(\displaystyle{\sum_{k=2}^{n+1}}\frac{1}{k}\leq\ln(n+1)\leq\displaystyle{\sum_{k=1}^n}\frac{1}{k}\).
Quand \(n\) tend vers \(+\infty\),
pour \(s > 1\), on a \(\displaystyle{\lim_{n\rightarrow+\infty}}\left(\frac{1}{n^{s-1}}-1\right)=-1\), la suite \((s_n)\), étant croissante et majorée, a une limite, la série \(\displaystyle{\sum_{n\geq1}}\frac{1}{n^s}\) est convergente ;
pour \(s\leq 1\), on retrouve le fait que la série \(\displaystyle{\sum_{n\geq1}}\frac{1}{n^s}\) est divergente.
Étude de la série de terme général \(u_n=\frac{1}{\sqrt{n^3-1}}(n\geq2)\)
On a, quand \(n\) tend vers \(+\infty\), \(u_n\sim\frac{1}{n^{\frac32}}\). La série est donc convergente.
Étude de la série de terme général \(u_n=\ln\left(1-\frac{1}{\sqrt{n}}\right)(n\geq2)\)
La série est à termes tous négatifs et, quand \(n\) tend vers \(+\infty\), \(u_n\sim-\frac{1}{\sqrt{n}}\). La série est donc divergente.
Étude de la série de terme général \(u_n=\frac{1}{n+\ln n}(n\geq1)\)
La série est à termes tous positifs, et on a, quand \(n\) tend vers \(+\infty\) :
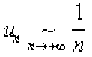. La série est donc divergente.Étude de la série de terme général \(u_n=\frac{1}{\sqrt{n}\ln n}(n\geq2)\)
On a, pour \(n\) assez grand, \(\ln n<\sqrt{n}\), d'où \(\frac{1}{\sqrt{n}\ln n}>\frac1n\). La série est donc divergente.
Étude de la série de terme général \(u_n=n^3\exp(-n)\)
Pour \(n\) assez grand, on a par exemple \(\exp^{(-n)}<\frac{1}{n^5}\) d'où \(\exp^{(-n)}n^3<\frac{1}{n^2}\), la série est convergente.
Dans les deux derniers cas, on a utilisé le premier théorème de comparaison.
On peut énoncer encore la règle suivante dite “Règle \(n^su_n\)”
Règle :
Pour qu'une série à termes positifs \(\sum u_n\) soit convergente, il suffit qu'il existe un réel \(s>1\) tel que la suite \((n'u_n)\) soit majorée.
Pour qu'une série à termes positifs \(\sum u_n\) soit divergente, il suffit qu'il existe un réel \(M\) strictement positif tel qu'on ait, à partir d'un certain rang, \(nu_n>M\).