Point matériel dans un champ de force uniforme
Durée : 10 mn
Note maximale : 10
Question
Un point matériel est soumis à une force uniforme et constante.
A l'instant \(t=0\), il se trouve au point \(M_0\) et sa vitesse est \(\vec{v_0}\).
Quelle est sa vitesse à l'instant \(t\neq0\)?
Quelle est sa position à l'instant \(t\) ?
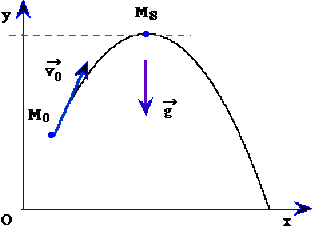
Montrez que la trajectoire du point matériel est une parabole de sommet \(M_S\) atteint lorsque la vitesse et l'accélération sont perpendiculaires.
Solution
On a \(\vec{F}(M,t)=\vec{F_0}\).
De l'équation fondamentale de la dynamique,
\(\vec{F}=m\frac{d^2\vec{OM}}{dt^2}\) avec \(m\neq0\)
on déduit que l'accélération du point matériel est uniforme et constante :
\(\frac{d^2\vec{OM}}{dt^2}=\frac{\vec{F_0}}{m}=\vec{a_0}\)
(1 point)
Sa vitesse varie donc linéairement au cours du temps : on trouve en effet par intégration
\(\frac{d\vec{OM}}{dt}=\vec{a_0}t+\vec{v_0}\)
L'hodographe est une droite parallèle à la direction de \(\vec{a_0}\).
(1 point)
La projection de la vitesse sur cette direction
\(\vec{a_0}.\frac{d\vec{OM}}{dt}\)
s'annule à l'instant \(t_S\), tel que
\(\vec{{a_0}^2}t_S+\vec{a_0}.\vec{v_0}=0\)
cet instant, la vitesse \(\vec{v_S}=\vec{v}(t_S)\) du point matériel est perpendiculaire à son accélération.
(1 point)
La position du point matériel par rapport à O varie quadratiquement en fonction du temps : elle est obtenue par une nouvelle intégration
\(\vec{OM}(t)=\vec{a_0}\frac{t^2}{2}+\vec{v_0}t+\vec{OM_0}\) ou \(\vec{M_0M}(t)=\vec{a_0}\frac{t^2}{2}+\vec{v_0}t\)
(1 point)
A l'instant \(t_S\), le point matériel se trouve au point \(M_S\) tel que
\(\vec{M_0M_S}=\vec{M_0M}(ts)=\vec{a_0}\frac{ts^2}{2}+\vec{v_0}t_S\)
(1 point)
Si on choisit l'instant \(t_S\) comme origine des temps et le point \(M_S\) comme origine de l'espace, la position du point matériel par rapport à \(M_S\) est repérée par
\(\begin{array}{rcl}\vec{M_SM}(t)&=&\vec{M_0M}(t).\vec{M_0M_S}\\&=&\vec{a_0}\frac{(t-t_S+t_S)^2}{2}+\vec{v_0}(t-t_S+t_S)-\left(\vec{a_0}\frac{{t_S}^2}{2}+\vec{v_0}t_S\right)\end{array}\)
soit
\(\vec{M_SM}(t-t_S)=\vec{a_0}\frac{(t-t_S)^2}{2}+(\vec{a_0}t_S+\vec{v_0})(t-t_S)=\vec{a_0}\frac{(t-t_S)^2}{2}+\vec{v_S}(t-t_S)\)
(2 points)
Le point matériel se déplace sur une parabole de sommet \(M_S\), atteint à l'instant \(t_S\), dont l'axe est parallèle à la direction de \(\vec{a_0}\).
En effet, comme \(\vec{a_0}.\vec{v_S}=0\), on a \(vec{a_0}.\vec{M_SM}=\vec{{a_0}^2}\frac{(t-t_S)^2}{2}\)
(1 point)
et \(\vec{v_S}.\vec{M_SM}=\vec{{v_S}^2}(t-t_S)\)
Par élimination de \((t - t_S)\) on obtient
\(\vec{a_0}.\frac{\vec{M_SM}}{a_0}=\left(\frac{a_0}{2}\vec{{v_S}^2}\right)\left(\vec{v_S}.\frac{\vec{M_SM}}{{v_S}^2}\right)\)
qui est la relation caractéristique liant les coordonnées d'un point d'une parabole repéré à partir de son sommet.
(2 points)