Equation fondamentale
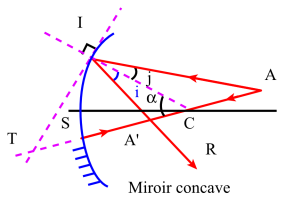
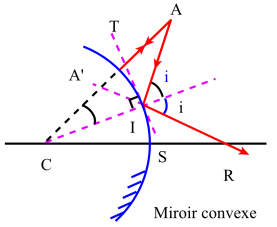
Soit un miroir sphérique de centre \(\mathrm C\) et de sommet \(\mathrm S\). Appelons \(\mathrm A\) un point lumineux quelconque de l'espace ; celui-ci est contenu dans un plan de section principale que l'on prend comme plan de figure.
Considérons un rayon incident quelconque \(\mathrm{AI}\) qui après réflexion se propage suivant \(\mathrm{IR}\). Si le miroir donne de \(\mathrm A\) une image[1] \(\mathrm{A'}\) celle-ci est nécessairement au point d'intersection de \(\mathrm{IR}\) avec le rayon lumineux \(\mathrm{AC}\), qui se réfléchit sur lui-même puisqu'il est normal au miroir (axe secondaire).
Traçons la tangente \(\mathrm{IT}\) au point d'incidence \(\mathrm I\) ; nous observons que les deux droites \(\mathrm{(IC)}\) et \(\mathrm{(IT)}\) ne sont autres que les deux bissectrices de l'angle \(\widehat{\mathrm{AIA'}}\), c'est-à-dire que les quatre points \(\mathrm A\), \(\mathrm{A'}\), \(\mathrm C\) et \(\mathrm T\) forment une division harmonique[2]
Dans le triangle \(\mathrm{CAI}\) on a la relation: \(\frac{\mathrm{CA}}{\sin~\mathrm i}=\frac{\mathrm{CI}}{\sin~\widehat{\mathrm{CAI}}}\) soit : \(\mathrm{CA}=\mathrm{CI}~\frac{\sin~\mathrm{i}}{\sin~\widehat{\mathrm{CAI}}}\)
et dans le triangle \(\mathrm{CA'I}\) la relation : \(\frac{\mathrm{CA'}}{\sin~\mathrm i}=-\frac{\mathrm{CI}}{\sin~(\pi-2\mathrm i-\widehat{\mathrm{CAI}})}=-\frac{\mathrm{CI}}{\sin~(2\mathrm i+\widehat{\mathrm{CAI}})}\)
d'où: \(\mathrm{CA'}=-\mathrm{CI}~\frac{\sin~\mathrm{i}}{\sin~(2\mathrm I+\widehat{\mathrm{CAI}})}\)
On en déduit la relation : \(\frac{\mathrm{CA}}{\mathrm{CA'}}=-\frac{\sin~(2\mathrm i~+~\widehat{\mathrm{CAI}})}{\sin~\widehat{\mathrm{CAI}}}\) dans le triangle \(\mathrm{TAI}\) on a la relation :
\(\frac{\mathrm{TA}}{\sin~\Big(\frac{\pi}2+\mathrm i\Big)}=\frac{\mathrm{TI}}{\sin~\widehat{\mathrm{TAI}}}~~~~\) on en déduit: \(~~\mathrm{TA}=\mathrm{TI}~\frac{\cos~\mathrm{i}}{\sin~\widehat{\mathrm{TAI}}}=\mathrm{TI}~\frac{\cos~\mathrm{i}}{\sin~\widehat{\mathrm{CAI}}}\)
et dans le triangle \(\mathrm{TA'I}\) : \(~~\frac{\mathrm{TA'}}{\sin~\Big(\frac{\pi}2-\mathrm i\Big)}=\frac{\mathrm{TI}}{\sin~\widehat{\mathrm{TA'I}}}~~\) d'où :
\(\mathrm{TA'}=\mathrm{TI}~\frac{\cos~\mathrm{i}}{\sin~\widehat{\mathrm{TA'I}}}=\mathrm{TI}\frac{\cos~\mathrm{i}}{\sin~(2\mathrm i~+~\widehat{\mathrm{CAI}})}\) soit : \(\frac{\mathrm{TA}}{\mathrm{TA'}}=\frac{\sin~(2\mathrm i~+~\widehat{\mathrm{CAI}})}{\sin~\widehat{\mathrm{CAI}}}\)
Des relations précédentes on déduit: \(\frac{\overline{\mathrm{CA}}}{\overline{\mathrm{CA'}}}=-\frac{\overline{\mathrm{TA}}}{\overline{\mathrm{TA'}}}\) soit: \(\frac{1}{\overline{\mathrm{CA}}}+\frac{1}{\overline{\mathrm{CA'}}}=\frac{2}{\overline{\mathrm{CT}}}\)
si on rapporte toutes les grandeurs algébriques à une même origine, le centre \(\mathrm C\) du miroir. On note par ailleurs que:
\(\overline{\mathrm{CT}}=\frac{\overline{\mathrm{CI}}}{\cos~\alpha}=\frac{\overline{\mathrm{CS}}}{\cos~\alpha}=\frac{\mathrm r}{\cos~\alpha}~\) ; en désignant par :
\(\mathrm r\) le rayon de courbure du miroir
\(\alpha=\widehat{\mathrm{ICT}}\)
Définition : Equation fondamentale des miroirs sphériques
\(\frac{1}{\overline{\mathrm{CA}}}+\frac{1}{\overline{\mathrm{CA'}}}=\frac{2~\cos~\alpha}{\mathrm r}~~~~\) avec \(~\mathrm r=\overline{\mathrm{CS}}\)
Cette relation représente l'équation fondamentale des miroirs sphériques.