Coordonnées des centres de gravité
Centre de gravité d'une courbe plane pesante
Le centre de gravité d'une courbe plane a ses coordonnées \(x_G\) et \(y_G\) définies par
\(x_G=\frac{\Sigma mx}{\Sigma m}~~~~y_G=\frac{\Sigma my}{\Sigma m}\)
Dans le cas d'une courbe symétrique par rapport à \(Ox,\) nous avons \(y_G = 0.\)
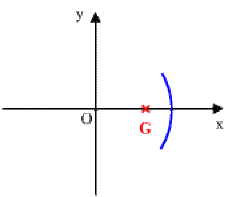
Si la courbe plane est homogène \((m = \lambda l),\) les coordonnées se réduisent à :
\(x_G=\frac{\int xdl}{\int dl}~~~~y_G=\frac{\int ydl}{\int dl}\)
Exemple : Centre de gravité d'un longueur
Déterminer le centre de gravité de la longueur de la demi-conférence \(x^2 + y^2 = R^2\) se trouvant au-dessus de l'axe \(Ox.\) (on prendra \(\lambda\) la masse linéique).
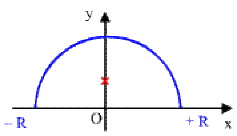
\(y_G=\frac{\int ydm}{\int dm}=\frac{\int y\lambda dl}{\int\lambda dl}=\frac{\int ydl}{\int ydl}\)
or \(dl=\sqrt{1+y'^2}dx\) avec \(y=\sqrt{R^2-x^2}\) et \(y'=\frac{-x}{\sqrt{R^2-x^2}}\)
d'où \(dl=\sqrt{1+\frac{x^2}{R^2-x^2}}dx=\frac R{\sqrt{R^2-x^2}}dx\)
soit \(y_G=\frac{R\int_{-R}^{+R}\sqrt{R^2-x^2}\frac{1}{\sqrt{R^2-x^2}}dx}{R\int_{-R}^{+R}\frac{dx}{\sqrt{R^2-x^2}}}\)
\(\color{red}y_G\color{black}=\frac{R[x]_{-R}^{+R}}{R[\arcsin\frac xR]_{-R}^{R}}=\color{red}\frac{2R}{\pi}\)
Centre de gravité d'aires planes
Le centre de gravité d'une aire plane a ses coordonnées \(x_G\) et \(y_G\) définies par :
\(x_G=\frac{\Sigma mx}{\Sigma m}~~~~y_G=\frac{\Sigma my}{\Sigma m}\)
Si la surface est homogène \((m = \sigma A),\) les coordonnées deviennent :
\(x_G=\frac{\int xdA}{\int dA}~~~~y_G=\frac{\int ydA}{\int dA}\)
Pour une aire symétrique par rapport à l'axe \(Ox\) et \(dA = y dx,\) nous aurons alors :
\(\color{red}x_G=\frac{\int xydx}{\int ydx}\) et \(y_G = 0\)
Exemple : Centre de gravité de l'aire d'un demi-cercle
Déterminer le centre de gravité de l'aire d'un demi-cercle.
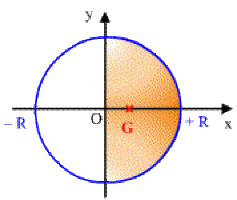
Par raison de symétrie, \(G\) se trouve sur l'axe \(Ox.\) Calculons donc \(x_G = OG.\)
Par définition
\(x_G=\frac{\int_0^Rx2ydx}{\int_0^R2ydx}=\frac{\int_0^Rx\sqrt{R^2-x^2}dx}{\int_0^R\sqrt{R^2-x^2}dx}\)
car \(y=\sqrt{R^2-x^2}\)
Posons \(\color{blue}x = R \sin\theta\Leftrightarrow dx = R \cos \theta d\theta\) et les bornes deviennent
\(\theta = \arcsin (x / R)\) \(x_1 = 0~~~~ \color{red}\theta_1= 0\\\color{black}x_2 = R~~~~\color{red}\theta _2= \pi/2\)
d'où :
\(x_G=\frac{R^3\int_0^{\pi/2}\cos^2\theta\sin\theta d\theta}{R^2\int_0^{\pi/2}\cos^2\theta d\theta}=\frac{R^3[-\frac{\cos^3\theta}{3}]_0^{\pi/2}}{\frac{R^2}{2}[\theta+\frac{\sin2\theta}{2}]_0^{\pi/2}}\)
\(\color{red}x_G\color{black}=\frac{\frac{R^3}{3}}{\frac{R^2\pi}{4}}=\color{red}\frac{4R}{3\pi}\)
Centre de gravité de volumes de révolution
Suite à la symétrie, le centre de gravité se trouve sur l'axe, par exemple pour une révolution autour de l'axe \(Ox.\)
\(x_G=\frac{\Sigma mx}{\Sigma m}\)
et dans le cas d'un volume homogène \((m = \rho V),\) nous avons :
\(\color{red}dm=\rho dV\) et \(\color{red}x_G=\frac{\int xdV}{\int dV}\)
Exemple : Centre de gravité d'une demi-sphère homogène
Déterminer le centre de gravité d'une demi-sphère homogène d'équation
\(x^2 + y^2 + z^2 = R^2\) se trouvant au-dessus du plan \(xOy.\)
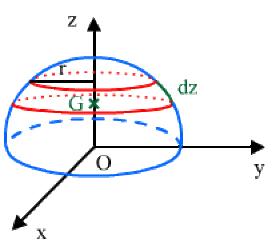
Le centre de gravité par raison de symétrie se trouve sur l'axe \(Oz.\)
\(z_G=\frac{\int zdV}{\int dV}\)
l'élément de volume étant \(dV = \pi R^2 dz = \pi (R^2 - z^2) dz\)
d'où \(z_G=\frac{\int_0^R\pi(R^2-z^2)zdz}{\int_0^R\pi(R^2-z^2)dz}=\frac{\pi[R^2\frac{z^2}2-\frac{z^4}4]_0^R}{\pi[R^2z-\frac{z^3}3]_0^R}\)
\(\color{red}z_G=\frac{3R}8\)