Moment d'inertie
Moment d'inertie par rapport à un axe (Δ)
Par définition le moment d'inertie \(I_{\Delta},\) par rapport à un axe \(_\Delta,\) d'un point matériel de masse \(m\) située à une distance \(r\) de \(_\Delta\) est :
\(\color{red}I_\Delta=mr^2\)
Un système de \(N\) points matériels de masses \(m_i,\) distants de \(r_i\) de l'axe \(D,\) aura pour moment d'inertie par rapport à \(_D\) :
\(\color{red}I_\Delta=\sum_{i=1}^Nm_ir_i^2\)
Dans le cas d'un corps solide constitué d'une infinité de points matériels, nous passerons à la limite suivante :
\(\color{red}I_\Delta=\lim_{N\rightarrow\infty}\sum_{i=1}^Nm_ir_i^2=\int r^2dm\)
Exemple : Moment d'inertie d'un cylindre homogène
Déterminer le moment d'inertie d'un cylindre homogène de masse volumique \(\sigma,\) de rayon \(R\) et de hauteur \(h\) par rapport à son axe.
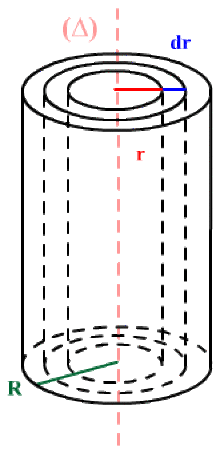
Choisissons pour masse élémentaire celle du tube d'axe \(\Delta\) de rayon \(r,\) de hauteur \(h\) et d'épaisseur \(dr.\)
\(dm = \rho dV = 2pr~\rho dr~ h\)
d'où \(I_\Delta = \int_0^Rr^2dm=\int_0^R2\pi\rho hr^3dr\)
\(=2\pi\rho h[\frac{r^4}4]_0^R=\pi\rho h\frac{R^4}2\)
\(\color{red}I_\Delta=\frac12MR^2\)
avec \(M = pR^2 h\rho\) la masse du cylindre
Théorème : d'Huyghens - Moment d'inertie par rapport à un axe (D) parallèle à l'axe (DG) qui passe par le centre de gravité
Le moment d'inertie d'un solide, par rapport à un axe \((_D),\) est égal au moment d'inertie de ce corps par rapport à un axe \(_{DG} ,\) parallèle à \(_D,\) passant par le centre de gravité augmenté du produit \(Md^2\) \((M\) étant la masse du solide et d la distance entre les deux axes)
\(\boxed{\color{red}I_D = I_{DG} + Md^2}\)
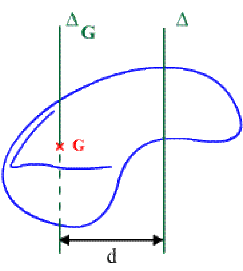
Par exemple pour le cylindre, le moment d'inertie par rapport à une de ses génératrices sera :
\(\color{red}I_\Delta\color{black}=I_{\Delta G}+Md^2=\frac12MR^2+MR^2=\color{red}\frac32MR^2\)
Moment d'inertie par rapport à un point
Le moment d'inertie d'un corps par rapport à un point \(O\) est égal à la demi-somme de ses moments d'inertie par rapports à trois axes perpendiculaires \((Ox,~ Oy,~ Oz)\) passant par le point \(O.\)
\(\boxed{\color{red}I_O = ( I_{Ox} + I_{Oy} + I_{Oz} ) / 2}\)
Exemple : Moment d'inertie d'une sphère homogène
Déterminer le moment d'inertie d'une sphère homogène de masse volumique \(\rho\) par rapport à son centre
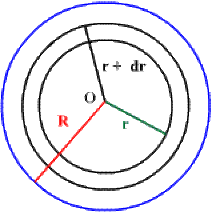
La masse élémentaire dm est comprise entre deux sphères de rayons \(r\) et \(r + dr,\) d'où
\(dm = \rho dV = \rho ( 4\pi r^2 dr)\)
et \(I_0=\int_0^Rr^2dm=4\pi\rho\int_0^Rr^4dr=4\pi\rho[\frac{r^5}5]_0^R=4\pi\rho\frac{R^5}5\)
\(\color{red}I_0=\frac35MR^2\)
car \(\textbf{M = 4\pi R^3 \rho}\)