Photocapteur
Partie
Question
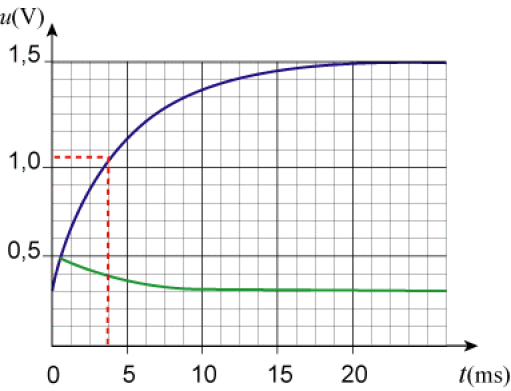
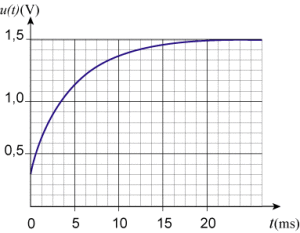
Pour mesurer des éclairements \(\mathcal{E}\), on utilise un photocapteur délivrant une tension \(\mathrm U(\mathcal{E})\). C'est un capteur linéaire du premier ordre, de constante de temps \(\tau\), de sensibilité \(\sigma=\mathrm{0,1 V/(W/m²)}\). Dans l'obscurité, le capteur a pour tension de sortie \(\mathrm U=0\). On soumet le photocapteur à un échelon d'éclairement \(\mathcal{E}_1\),\(\mathcal{E}_2\). La courbe de réponse du capteur est donnée ci-dessous.
Déduire de cette courbe :
la valeur de l'éclairement initial \(\mathcal{E}_1\) et de l'éclairement final \(\mathcal{E}_2\).
la constante de temps \(\tau\) du capteur.
On soumet le capteur à l'éclairement \(\mathcal{E}_2\) pendant une durée \(\delta T\), puis on revient à l'éclairement initial \(\mathcal{E}_1\)( créneau de largeur \(\delta T\)). Pour \(\delta T_1=\mathrm{1 s}\), puis \(\delta T_2=\mathrm{0,5 ms}\), déterminer la réponse du capteur à la fin du créneau, en utilisant la courbe \(U(t)\) ci-dessus . En déduire l'allure de la réponse du capteur pour les deux largeurs de créneau proposées.
Aide simple
Le capteur est supposé être en régime statique avant le début de l'échelon
Aide détaillée
Le capteur est linéaire, et sa réponse \(U\) est nulle dans l'obscurité (\(\mathcal{E}=0\)), donc \(U=\sigma.\mathcal{E}\) en régime statique.
Solution simple
Echelon :\(\mathcal{E}_1=\mathrm{3 W.m}^{-2}\); \(\displaystyle{\mathcal{E}_2=\frac{U_2}{\sigma}=15\mathrm{ W.m}^{-2}}\); \(\tau=\mathrm{4 ms}\)
Créneau \(\delta T_1\): réponse en créneau de \(\mathrm{0,3}\) à \(\mathrm{1,5 V}\).
Créneau \(\delta T_2\): réponse exponentielle croissante de \(\mathrm{0,3}\) à \(\mathrm{0,43 V}\), de \(t=0\) à \(t=\delta T_2\), puis exponentielle décroissante de \(\mathrm{0,43}\) à \(\mathrm{0,3 V}\)
Solution détaillée
La variation d'éclairement appliquée au photocapteur peut être considérée comme un échelon de \(\mathcal{E}_1\) à \(\mathcal{E}_2\).
Le capteur est linéaire, et sa réponse \(U\) est nulle dans l'obscurité (\(\mathcal{E}=0\)), donc \(U=\sigma.\mathcal{E}\) en régime statique.
Il est supposé être en régime statique avant le début de l'échelon, donc sa réponse au début de l'échelon est \(U_1=\sigma.\mathcal{E}_1\), d'où : \(\displaystyle{\mathcal{E}_1=\frac{U_1}{\sigma}=\mathrm{3 W.m}^{-2}}\).
En fin de courbe, la valeur finale correspondant au nouveau régime statique est pratiquement atteinte, d'où : \(\displaystyle{\mathcal{E}_2=\frac{U_2}{\sigma}=\mathrm{15 W.m}^{-2}}\)
Puisque le photocapteur est un capteur linéaire du premier ordre, sa réponse va être :
\(u(t)=\mathrm{A.e}^{-t/\tau}\) + solution particulière de l'équation complète
comme la grandeur à mesurer (éclairement du malade) est constante, on cherche une solution particulière constante, ce qui donne \(u=U_2\), d'où la solution générale :
\(u(t)=\mathrm{A.e}^{-t/\tau}+U_2\)
pour déterminer la constante \(\mathrm A\), il faut utiliser les conditions initiales ; si on prend comme origine des dates l'instant où le photocapteur est soumis à l'éclairement \(\mathcal{E}_2\), à \(t=0\) le photocapteur avait pour réponse \(U_1\):
\(u(0)=U_1=\mathrm A+U_2\), d'où \(\mathrm A=U_1-U_2\);
finalement : \(u(t)=(U_1-U_2)\mathrm e^{-t/\tau}+U_2=-\mathrm{1,2e}^{-t/\tau}+\mathrm{1,5}\)
pour \(t=\tau\), la réponse sera donc \(u(t)=-\mathrm{1,2e}^{-t/\tau}+\mathrm{1,5}=\mathrm{1,06 V}\)ce qui correspond sur la courbe \(u(t)\) à \(\tau=\mathrm{4 ms}\)(en rouge sur la courbe).
Réponse à un créneau :
\(\delta T_1=\mathrm{1 s}\gg\tau\): la réponse \(U_2\) peut être considérée comme atteinte avant que l'intervalle d'éclairement \(\mathcal{E}_2\) soit fini. Le capteur a donc une réponse pratiquement en forme de créneau, variant de \(\mathrm{0,3}\) à \(\mathrm{1,5 V}\).
\(\delta T_2=\mathrm{0,5 ms}<\tau\): la réponse pour \(t=\delta T_2\) peut être lue sur la courbe \(u(t)\) : \(u(\delta T_2)=\mathrm{0,43 V}\); sa forme est exponentielle, et croissante ; quand l'éclairement revient à la valeur \(\mathcal{E}_1\), le capteur est soumis à un nouveau créneau , négatif, et la valeur limite de la réponse devient \(U_1\)
la courbe est donc une exponentielle décroissante, allant de la valeur initiale \(u(\delta T_2)=\mathrm{0,43 V}\) à la valeur finale \(U_1=\mathrm{0,3 V}\)(courbe verte).
