Propagation d'un signal représenté par sa série de Fourier
Les schémas ci-dessous représentent les 3 premiers termes de la série de Fourier d'un signal carré dissymétrique ainsi que la somme de ces 3 premiers termes.
En \(z=0\), la vibration de la source est périodique et représentée (par exemple) par sa série de Fourier :
\(\displaystyle{ \psi(z = 0 , t) = F(t) = \sum_{n = - \infty}^{n = + \infty} C_n . \mathrm{e}^{\mathrm{i} . n . \frac{2 \pi}{T} . t} = \sum_{n = - \infty}^{n = + \infty} C_n . \mathrm{e}^{\mathrm{i} . \omega_n . t} } \textrm{ avec } \omega_n = n . \omega_1 = n . \frac{2 . \pi}{T}\)
La propagation de la vibration de cette source s'exprime par exemple :
\(\displaystyle{\psi(z,t) = \sum_{n = - \infty}^{n = + \infty} C_n . \mathrm{e}^{\mathrm{i} (\omega_n . t - K_n . z)} \mathrm{ }\mathrm{ }\textrm{ o\`u }\mathrm{ } V_n = \frac{\omega_n}{K_n}} \textrm{ est la vitesse de l'harmonique}\)
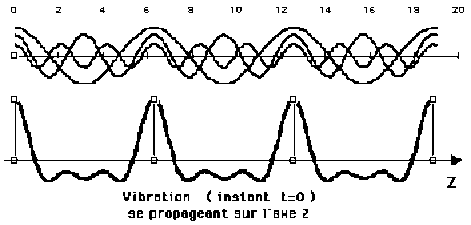
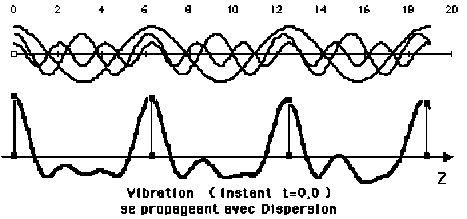
Les 2 schémas ci-dessus représentent respectivement la propagation dans le cas d'un milieu non-dispersif et dans le cas d'un milieu dispersif. Consultez aussi les simulations correspondantes :
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.