Relations de dispersion et propagation
L'équation de propagation des ondes électromagnétiques : \(~ \frac{\partial^2 \vec E}{\partial z^2} = \varepsilon . \mu . \frac{\partial^2 \vec E}{\partial t^2} ~\) comme l'équation des cordes vibrantes : \(~ \frac{\partial^2 \psi}{\partial z^2} = \frac{\rho}{T} . \frac{\partial^2 \psi}{\partial t^2} ~\), ou comme le système des \(N\) équations que l'on obtient dans le cas d'un système à \(N\) degrés de liberté admettent des solutions traduisant aussi bien les phénomènes de vibration que les phénomènes de propagation.
On a d'ailleurs établi (dans le cas des ondes électromagnétiques, mais cette propriété est générale et ne dépend pas de la nature de l'onde) qu'une onde stationnaire peut s'exprimer comme superposition d'ondes harmoniques de même amplitude, l'une progressive, l'autre régressive.
Les relations entre \(\omega\) et \(K\) que l'on établit en considérant des solutions de type : mode propre, ou de type : onde stationnaire, sont donc les mêmes relations que l'on obtient à partir des solutions de type : propagation.
A titre d'exemple, nous allons toutefois montrer que la relation de dispersion du système de \(N\) masses et \(N+1\) ressorts peut s'obtenir directement, en recherchant des solutions de type propagation au système des \(N\) relations.
L'équation de la n-ième masse s'écrit :
\(\begin{array}{lll} m . \ddot \psi^n & = & \frac{T}{a} . [\psi^{n+1} - \psi^n] - \frac{T}{a} . [\psi^n - \psi^{n-1}] \\ & = & \frac{T}{a} (\psi^{n+1} + \psi^{n-1} - 2 . \psi^n) \end{array}\)
Si l'on fait se propager une onde sinusoïdale de pulsation \(\omega\), cette onde va mettre en vibration successivement toutes les masses du système.
En supposant qu'à l'origine la vibration est de type : \(\cos (\omega . t)\) , à l'ordonnée \(z_n\) correspondant à la n-ième masse : \(z_n = n.a\) (où \(a\) est la distance entre \(2\) masses consécutives).
La vibration sera décrite par : \(~~ \psi^n(t) = A . \cos [\omega.t - K.z_n] = A . \cos [\omega.t - K.n.a]\)
et de même : \(~~ \psi^{n+1}(t) = A . \cos [\omega.t - K.(n+1).a]\)
et : \(~~ \psi^{n-1}(t) = A . \cos[\omega.t - K.(n-1).a]\)
d'où l'on tire : \(~~ \psi^{n+1} + \psi^{n-1} = 2 .\psi^n. \cos (K.a)\)
En reportant cette somme dans l'équation de départ, on obtient la relation :
\(m . \ddot \psi^n = \frac{2 . T}{a} . [1 - \cos(K.a)] . \psi^n\)
soit : \(~ \ddot \psi^n = \frac{2 . T}{m . a} . 2 \sin^2 \Big( \frac{K . a}{2} \Big) . \psi^n ~\) qui admet une solution harmonique, dont la pulsation satisfait la relation :
\(\omega^2 = \frac{4 . T}{m . a} . \sin^2 \Big( \frac{K . a}{2} \Big)\)
La vitesse est donc : \(~~ V = \frac{\omega}{K} = 2 . \sqrt{\frac{T}{m . a}} . \frac{\sin \Big( \frac{K . a}{2} \Big)}{K}\)
Cette relation entre \(\omega\) et \(K\) est exactement celle qui avait été trouvée, dans le cas des modes propres, entre la pulsation et le module du vecteur d'onde (même relation, mais avec l'indice \(p\)).
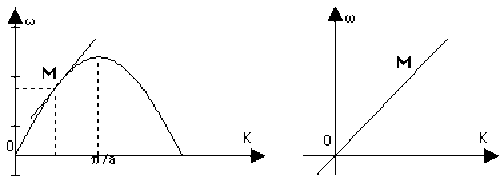
Le rapport \(\frac{\omega}{K}\) qui représente la vitesse de propagation en \((\omega,K)\) est défini sur le graphe \(\omega(K)\) par la pente de la droite \(OM\).
Si le milieu est dispersif, cette pente varie avec \(K\).
Dans le système dispersif considéré ici, la vitesse de propagation est plus grande pour les faibles valeurs de \(K\) (ou de la pulsation) que pour les plus grandes valeurs de \(K\) (ou de la pulsation).
Les harmoniques de rang élevé (i.e. de pulsation élevée) se propagent donc moins vite que ceux de rang inférieur.
L'allure de la courbe de dispersion permet ainsi de comprendre la propagation.
Inversement, connaissant la forme de la propagation, on peut en déduire si les termes de fréquence élevée sont plus ou moins rapides que ceux de basse fréquence. Faire cette analyse à propos des graphes du paragraphe précédent représentant la propagation d'un créneau carré avec dispersion.
Reprenons l'exemple étudié au § C.3.a (Propagation d'un battement) mettant en évidence la vitesse de phase et la vitesse de groupe.
Soit \(M\) le point du graphe ci-dessus correspondant à la pulsation moyenne :
\(\omega_M = \frac{\omega_1 + \omega_2}{2}\)
La pente de la droite \(OM\) représente alors la vitesse de phase \(V_{\varphi}\).
Si l'écart des pulsations \(\omega_1\) et \(\omega_2\) est assez faible, la vitesse de groupe est alors :
\(\displaystyle{V_G = \frac{\omega_1 - \omega_2}{K_1 - K_2} \approx \left( \frac{\partial \omega}{\partial K} \right)_M}\)
La vitesse de groupe est la pente de la tangente en \(M\) à la courbe de dispersion.
On voit en particulier que la vitesse de groupe peut se trouver très différente de la vitesse de phase, selon la position de \(M\) sur la courbe de dispersion.