Propagation à partir de sources non-ponctuelles
L'application qui suit est une formulation théorique des phénomènes de diffraction et d'interférence. Le cas des interférences ne sera pas traité ici mais sera étudié en Travaux Dirigés et en Travaux Pratiques. Nous indiquerons simplement ici (voir la partie "Schémas: diffraction/interférences") l'allure de la variation :
de la densité d'amplitude de diffraction en fonction de l'angle (pour différents diamètres de source),
de la densité d'amplitude d'interférences en fonction de l'angle (pour plusieurs valeurs de la distance entre les centres des deux sources qui interfèrent).
Diffraction par une fente de largeur D.
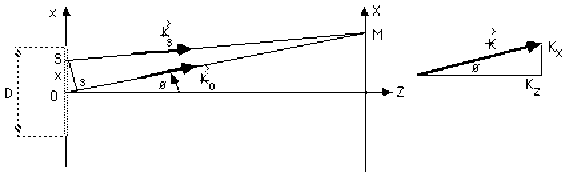
On étudie la propagation dans le plan \((XOZ)\) de la vibration émise par une source.
La source considérée est une fente de largeur \(D\), située dans le plan \(Z=0\), et parallèle à l'axe \(OY\) (l'axe \(OY\) est équidistant des bords de la fente).
On suppose que tous les points de cette source oscillent en phase.
La vibration d'un point quelconque \(S (x, Z=0)\) de la source sera représentée en notation complexe par une fonction : \(\psi(Z=0,t) = A . \mathrm{e}^{\mathrm{i}.\omega t}\) où \(A\) est un facteur d'amplitude donné [ avec ici : \(A = \psi(Z=0,t=0)\) ].
Dans le plan émetteur, on peut donc représenter le facteur d'amplitude de la vibration de la source par la fonction \(F\), définie par :
\(\begin{array}{lll} F(x) = A & \mathrm{ pour } & x\in \left[ - \frac{D}{2} ~ , + \frac{D}{2} \right] \\ F(x) = 0 & \mathrm{ pour } & x \notin \left[ - \frac{D}{2} ~ , + \frac{D}{2} \right] \end{array}\)
Cette source émet dans toutes les directions \(\theta\), i.e. \(\forall K_x \in [-K, +K]\) si la norme du vecteur d'onde reste constante (et égale à \(K\)) quelle que soit la direction d'émission considérée.
Plus généralement, on peut considérer que \(K_x \in [-i, +i]\) , quitte à ce que certaines valeurs de \(K_x\) aient une contribution nulle.
L'amplitude de vibration de cette source étendue n'est pas constante en fonction de \(\theta\) (et donc de \(K_x\) ) car elle ne possède pas la symétrie cylindrique.
Pour exprimer la propagation à partir de cette source étendue, représentée par le facteur d'amplitude \(F(x)\), on peut considérer que chacun des points \(S\) (d'abscisse \(x \in \Big[ - \frac{D}{2} ~, + \frac{D}{2} \Big]\) sur la droite \(Ox\) du plan \((xOy)\)) de cette source émet une vibration dans toutes les directions, avec une symétrie cylindrique.
On admettra donc que la norme de \(\vec K_S\) (vecteur d'onde provenant de \(S\)) reste constante dans toutes les directions d'émission, et pour tous les points \(S\) de la source. On notera \(|| K ||\) cette norme, et on notera \(\vec K_O\) un vecteur d'onde provenant de \(O\).
Ne contribuent à l'amplitude de vibration arrivant en \(M\) que les vecteurs d'onde dirigés vers \(M\). L'amplitude élémentaire arrivant en \(M\) à l'instant \(t\) en provenance du point \(S\) est donc :
\(\mathrm{d} \psi_S (M, t) = [F(x)] . \mathrm{e}^{\mathrm{i} ~ ( \omega . t ~ - ~ \vec K_S . \overrightarrow{SM})} . \mathrm{d}x\)
En notant \(s\) la projection de \(S\) sur la direction \(OM\) et à condition d'observer à distance constante (sur un cercle, ou dans un plan situé à une distance assez grande par rapport à la dimension de la source), on a :
\(- \vec K_S . \overrightarrow {SM} \cong - \vec K_O . \overrightarrow{sM} = - \vec K_O . \overrightarrow {sO} - \vec K_O . \overrightarrow {OM} = + \vec K_O . \overrightarrow {Os} - \vec K_O . \overrightarrow {OM}\)
En notant \(\theta\) l'angle : \(\theta = (\overrightarrow{OZ}, \overrightarrow{OM}) = (\overrightarrow{OZ}, \vec K_O)\)
On a : \(O_S = x . \sin \theta\)
\(K_X = K_O ~ \sin \theta ~~\) d'où : \(\vec K_O . \overrightarrow{Os} = K_x . x\)
ce qui permet de trouver :
\(\mathrm{d} \psi_S (M, t) = F(x) . \mathrm{e}^{\mathrm{i} ~ ( \omega . t ~ + ~ K_x . x ~ - ~ \vec K_O . \overrightarrow{OM})} . \mathrm{d}x\)
soit encore :
\(\mathrm{d} \psi_S (M, t) = F(x) . \mathrm{e}^{\mathrm{i} ~ (K_x . x)} . \mathrm{e}^{\mathrm{i} ~ ( \omega . t ~ - ~ \vec K_O . \overrightarrow{OM})} . \mathrm{d}x\)
Dans cette expression, le produit scalaire \(\vec K_O . \overrightarrow{OM} = K . OM\) ne dépend pas de \(x\).
L'intégration sur la source, i.e. sur toutes les valeurs de \(x\), donne donc :
\(\begin{array}{l} {\psi_S (M, t) = \left[ \int_{- \infty}^{+ \infty} F(x) . \mathrm{e}^{\mathrm{i} ~ (K_x . x)} . \mathrm{d}x \right] . \mathrm{e}^{\mathrm{i} ~ ( \omega . t ~ - ~ \vec K_O . \overrightarrow{OM})} } \end{array}\)
Interprétation
Pour interpréter ce résultat, il est nécessaire d'utiliser la définition de la Transformée de Fourier \(f(K_x)\) de la fonction \(F(x)\) et de remarquer que :
\(\displaystyle{ \frac{1}{2 \pi} \int_{- \infty}^{+ \infty} F(x) . \mathrm{e}^{\mathrm{i} ~ (K_x . x)} . \mathrm{d}x = f(- K_x)}\)
On peut calculer la Transformée de Fourier :
\(\displaystyle{ f(K_x) = \frac{1}{2 \pi} \int_{- \infty}^{+ \infty} F(x) . \mathrm{e}^{- \mathrm{i} ~ (K_x . x)} . \mathrm{d}x}\)
On trouve, tous calculs faits :
\(\displaystyle{ f(K_x) = \frac{A}{2 \pi} \int_{- D/2}^{+ D/2} \mathrm{e}^{- \mathrm{i} ~ (K_x . x)} . \mathrm{d}x = \frac{A}{2 \pi K_x} ~ . ~ \sin \Big(K_x . \frac{D}{2}\Big)}\)
qui est donc une fonction de \(K_x\) paire.
Par suite :
\(\displaystyle{\frac{1}{2 \pi} \int_{- \infty}^{+ \infty} F(x) . \mathrm{e}^{\mathrm{i} ~ (K_x . x)} . \mathrm{d}x = f(- K_x) = f(K_x)}\) .
Propriété :
La densité de l'amplitude résultante arrivant en \(M\) à l'instant \(t\), en provenance de cette source étendue s'exprime donc simplement par :
\(\psi (M, t) = 2 \pi . f(K_x) . \mathrm{e}^{\mathrm{i} ~ ( \omega . t ~ - ~ \vec K_O . \overrightarrow{OM})}\)
Tout se passe donc comme si la source étendue émettait depuis son centre \(O\), avec une densité d'amplitude \(2\pi . f(K_x)\) :
i.e. fonction de la direction d'observation \(\theta\) , et donnée par le spectre de Fourier \(f(K_x)\) de la fonction \(F(x)\), où la fonction \(F\) représente dans le plan d'émission \((Z=0)\) le facteur d'amplitude en fonction de \(x\).
\(\psi (M,t)\) représente la densité d'amplitude de la vibration en \(M\) à l'instant \(t\), puisque \(f(K_x)\) est la densité d'amplitude de la vibration émise selon la direction du vecteur d'onde de composante \(K_x\) .
La démonstration de ces résultats (faite ici sur l'exemple particulier de l'émission par une fente) reste valable à condition que la fonction \(F(x)\) représentant l'amplitude soit réelle et paire, car on peut montrer que :
\(F(x)\) paire \(~~ \Rightarrow ~~\) \(f(K_x)\) paire ;
\(F(x)\) réelle \(~~ \Rightarrow ~~\) \(f(K_x)\) hermitienne, i.e. : \(f(K_x) = \overline{f(-K_x)}\) .
Calcul des déphasages
Chaque point émetteur, i.e. chaque point du plan \((Z = 0)\) affecté de son coefficient d'amplitude \(F(x)\), émet une vibration que l'on observe dans la direction \(\theta\) (correspondant à une valeur \(K_x\) déterminée).
Cet angle \(\theta\) introduit un déphasage entre les vibrations provenant des différents points de la source : ce déphasage est le produit de \(K\) par la différence de longueur des trajets, entre les différents points de la source [par exemple, le déphasage entre un point d'abscisse \(x\) et le centre \(O\) de la source est égal à \(+K.x.\sin \theta\), donc à \(+K_x.x\)].
Ce qui revient (en notation complexe) à considérer que l'amplitude arrivant en \(M\) depuis un point \(S\) (abscisse \(x\)) de la source est multipliée par le facteur de phase : \(\mathrm{e}^{+ \mathrm{i} . K_x . x}\)
On peut alors déterminer l'expression de l'amplitude en \((M,t)\) en faisant la somme de ces amplitudes \(F(x) . \mathrm{e}^{+ \mathrm{i} . K_x . x}\) en provenance des différents points de la source (chacune d'elle étant affectée par son déphasage). Le résultat est identique à celui déterminé ici par Transformation de Fourier : cette amplitude en \((M, t)\) est proportionnelle au spectre \(f(K_x)\) de la fonction \(F(x)\).
Remarque :
Les 2 méthodes proposées donnent des résultats équivalents, mais :
La méthode par Transformée de Fourier est beaucoup plus simple que le calcul direct de la somme des amplitudes avec déphasages. Elle est également beaucoup plus puissante.
Dans le calcul de la Transformée de Fourier \(f(K_x)\) de la source \(F(x)\), on effectue la sommation sur toute la source, raison pour laquelle le spectre \(f(K_x)\) fournit une information globale sur la propagation à partir d'une source étendue.
L'appareil de mesure centré au point \(M\) possède lui-même une certaine largeur, de sorte qu'il détecte non pas la densité à la valeur \(K_x\) correspondant au point \(M\), mais un domaine d'émission \(\Delta \theta\), i.e. une bande spectrale \(\Delta K_x\) autour de la valeur \(K_x\) correspondant au point \(M\).
Si, par exemple, la sensibilité de cet appareil de mesure est supposée constante sur ce domaine \(\Delta K_x\), la densité \(\psi(M,t)\) permet d'exprimer la valeur de l'amplitude \(S(M,t)\) mesurée sur le détecteur centré en \(M\) :
\(\displaystyle{S(M, t) = \int_{(\Delta K_x)} \psi(M,t) . \mathrm{d} K_x = \left[ \int_{(\Delta K_x)} f(K_x) .\mathrm{d}K_x \right] . \mathrm{e}^{\mathrm{i} ~ ( \omega . t ~ - ~ \vec K_O . \overrightarrow{OM})} }\)
qui représente une moyenne sur \(\Delta K_x\) effectuée par cet appareil de mesure.
Les courbes de diffraction représentées dans la partie "Schémas : diffraction/interférences" ont été calculées pour des sources de largeur différentes : ces largeurs ont toutes été choisies multiples de la longueur d'onde \(\lambda\).
Les autres courbes de la partie "Schémas : diffraction/interférences" représentent les interférences entre deux sources identiques, de même largeur \(D\). Elles ont été calculées pour différents écartements entre les centres de ces deux sources : ces écartements ont tous été choisis multiples de la largeur \(D\) de chacune des sources. Le plus petit de ces écartements est égal à \(D\), ce qui signifie que les sources sont alors jointives et n'en constituent plus qu'une seule.