Convergence d'une suite vers un réel
Intuitivement la suite \((u_n)\) converge vers un réel \(l\) si \(u_n -l\) est petit quand \(n\) est grand, ce qui veut dire "aussi petit que l'on veut" mais pas "de plus en plus petit".
Définition : Convergence d'une suite vers un réel
Soit \((u_n)\) une suite réelle et soit \(l\) un réel ; on dit que \((u_n)\) converge vers \(l\) quand \(n\) tend vers \(+\infty\) si l'une des propriétés 1. 2. 3. équivalentes suivantes est vérifiée.
Pour tout voisinage \(V\) de \(l\), il existe un rang \(N\), tel que \(u_n\) appartienne à \(V\) pour tout entier \(n\) supérieur ou égal à \(N\).
Tout intervalle ouvert contenant \(l\) contient tous les termes de la suite sauf pour un nombre fini d'indices.
Quel que soit \(\epsilon>0\) , il existe \(N\in \mathbb N\) tel que \(n \geq N\) entraîne \(\vert u_n-l\vert<\epsilon\).
Il est bien évident que l'entier \(N\) dépend de la suite \((u_n)\) et de \(\epsilon\).
Elle s'écrit en langage formalisé :
\(\displaystyle{\forall\epsilon>0,\quad\exists N\in\mathbb N,\quad\forall n\in\mathbb N,\;(n\geq N\Rightarrow\vert u_n-l\vert<\epsilon)}\)
La propriété (c) peut être exprimée:
en représentation axiale
en représentation graphique
Complément : Les représentations
La propriété (c) exprime:
en représentation axiale qu'il n'y a qu'un nombre fini de termes hors de l'intervalle \(]l-\epsilon,l+\epsilon[\) ou encore que tous les \(u_n\) pour \(n\geq N\) appartiennent à l'intervalle \(]l-\epsilon,l+\epsilon[\),
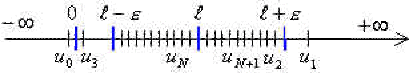
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
en représentation graphique qu'il n'y a qu'un nombre fini de points \((n,u_n)\) hors de la bande \(N\times]l-\epsilon,l+\epsilon[\) ou encore que tous les points \((n,u_n)\) pour \(n\ge N\) appartiennent à la bande \(N\times]l-\epsilon,l+\epsilon[\).
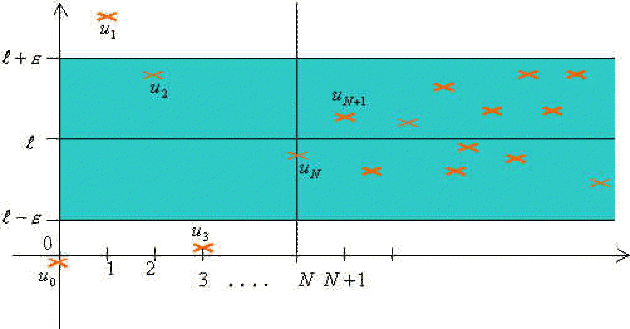
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Remarque :
On définit le même concept de limite en prenant indifféremment les inégalités \(n\geq N\) ou \(n> N\) et \(\vert u_n-l\vert<\epsilon\) ou \(\vert u_n-l\vert\leq\epsilon\) .
Exemple :
Il s'agit non de donner une méthode d'étude des suites (les théorèmes efficaces seront vus ultérieurement), mais d'effectuer des calculs de l'entier \(N\) en fonction de \(\epsilon\).
La suite \(\displaystyle{\left(\frac{1}{n}\right)_{n\geq 1}}\) converge vers \(0\).
Soit \(\epsilon>0\), on cherche un rang \(N(\epsilon)\) tel que l'on ait \(\displaystyle{0<\frac{1}{n}<\epsilon}\) pour \(n\geq N(\epsilon)\).
Il suffit de prendre \(\displaystyle{N(\epsilon)=\left[\frac{1}{\epsilon}\right]+1}\).
Pour \(\epsilon= 10^{-2}\) on a \(N(10^{-2} ) = 101\).
La suite \(\displaystyle{\left(\frac{1}{n+(-1)^n\sqrt n}\right)_{n\geq 2}}\) converge vers 0.
La réalisation de la condition \(\displaystyle{0<\frac{1}{n+(-1)^n\sqrt n}<\epsilon}\) pour \(n\geq N(\epsilon)\) est plus difficile que dans le cas précédent car cette suite n'est pas monotone.
On peut utiliser le fait que la suite \(\displaystyle{\left(\frac{1}{n+(-1)^n\sqrt n}\right)_{n\geq 2}}\) est majorée par la suite \(\displaystyle{\left(\frac{1}{n-\sqrt n}\right)_{n\geq 2}}\) et cette dernière suite vérifie \(\displaystyle{0<\frac{1}{n-\sqrt n}\leq\frac{2}{n}}\) pour \(n\geq 4\).
Il suffit alors de réaliser \(\displaystyle{0<\frac{2}{n}<\epsilon}\), soit \(\displaystyle{n>\frac{2}{\epsilon}}\) avec \(n\geq 4\).
On peut donc prendre \(\displaystyle{N(\epsilon) =\textrm{max}\left(\left[\frac{2}{\epsilon}\right]+1,4\right)}\); pour \(\epsilon= 10^{-2}\) on a \(N(10^{-2}) =201\).
Pour tout \(x\) réel la suite \((x_n)\) des approximations décimales par défaut d'ordre \(n\) converge vers \(x\).
On a en effet \(\displaystyle{x_n\leq x< x_n+10^{-n}}\) d'où \(\vert x-x_n\vert<10^{-n}\).
On peut donc prendre \(\displaystyle{N(\epsilon)=\left[\log_{10}\frac{1}{\epsilon}+1\right]}\);
pour \(\epsilon= 10^{-2}\) on a \(N(\epsilon) = 2\).
Remarque :
L'entier \(N(\epsilon)\) n'est, bien évidemment, pas unique, tout entier supérieur convient. On s'efforcera de chercher le "meilleur", c'est à dire le plus petit.