Exemples de cas où la condition de continuité n'est pas réalisée
On se propose d'étudier différents cas dans lesquels, pour des raisons diverses, la condition représentée par l'assertion :
\(\displaystyle{\forall\epsilon>0,\exists\eta>0,\forall x\in I\quad(\left\vert x-x_0 \right\vert<\eta\Rightarrow\left\vert f(x)-f(x_0)\right\vert<\epsilon)}\)
n'est pas réalisée. On verra que, dans certains cas, on peut étendre la notion de continuité. On étudiera aussi un cas où l'étude est réalisée au voisinage de \(+\infty\).
Les exemples qui suivent permettent de concevoir des notions dont nous allons ensuite donner une définition précise.
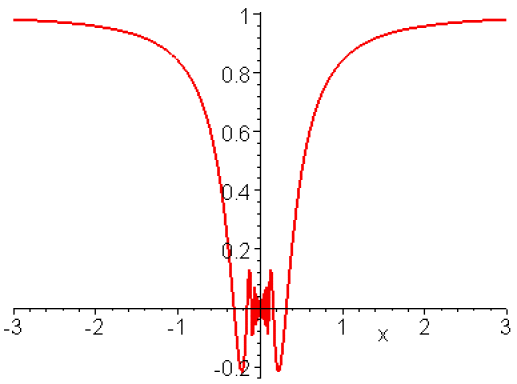
Exemple : a. Prolongement par continuité
Soit \(\displaystyle{f_1 :\mathbb R^*\to\mathbb R\quad x\mapsto x\sin\left(\frac{1}{x}\right)}\)
Le point \(0\) n'appartient pas à l'ensemble de définition, on ne peut donc pas a priori parler de continuité.
Cependant la fonction \(f_1\) vérifiant, pour tout \(x\) réel non nul, l'inégalité \(\left\vert f_1(x)\right\vert\leq\left\vert x\right\vert\), satisfait, au voisinage de \(0\), à la condition :
\(\displaystyle{\forall\epsilon>0,\exists\eta>0,\forall x\in\mathbb R^*\quad(\vert x\vert<\eta\Rightarrow\left\vert f_1(x)\right\vert\leq\epsilon)}\),
il suffit en effet de prendre \(\eta=\epsilon\).
La fonction \(f_1^*\), définie par :
\(\displaystyle{f_1^*(x)=x\sin\left(\frac{1}{x}\right)\quad x\neq0,\quad f_1^*(0)=0}\)
est donc continue en tout point de \(\mathbb R\) en particulier en \(0\).
Dans un tel exemple on dira que l'on a prolongé par continuité la fonction au point \(0\), et la valeur \(0\), donnée à \(f_1\textrm{ en }0\), pour la rendre continue sera appelée limite; ces deux concepts, qui sont donc liés, seront définis et étudiés plus tard.
Exemple : b. Continuité à droite et à gauche
Soit \(\displaystyle{f_2 :\mathbb R\to\mathbb R,\quad x\mapsto E(x)=[x]}\)
On étudie \(f_2\) au voisinage de 1, on a
\(\left\{\begin{array}{ll}f_2(x)=0&\textrm{ si } 0\le x<1 \\f_2(x)=1&\textrm{ si } 1\leq x<2\end{array}\right.\).
Contrairement à l'exemple précédent \(f_2\) est définie au point \(1\), elle n'est pas continue en ce point, ce qui se traduit sur le graphe par un saut.
Pourtant, si \(1\leq x<2, f_2(x)=1= f_2(1)\) on a donc :
\(\displaystyle{\forall\epsilon>0,\exists\eta=\frac{1}{2},\forall x\in\mathbb R\quad(1\leq x<1+\eta\Rightarrow\left\vert f_2(x)-f_2(1)\right\vert<\epsilon)}\).
On dira que \(f_2\) est continue à droite et ce concept sera défini plus tard. A gauche il ne peut être question de continuité puisque \(f_2(x)=0\) pour \(0\leq x <1\), mais on remarque que :
\(\displaystyle{\forall\epsilon>0,\exists\eta=\frac{1}{2},\forall x\in\mathbb R\quad(1-\eta< x<1\Rightarrow\left\vert f_2(x)\vert<\epsilon\right)}\),
d'où le concept de limite à gauche.
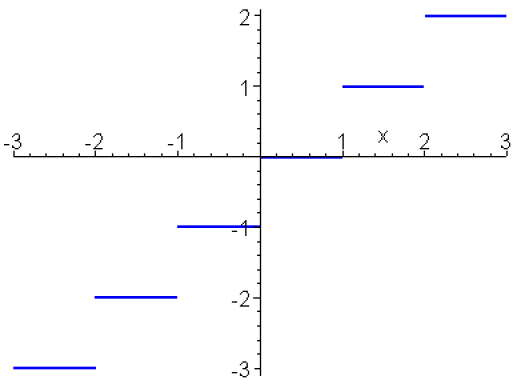
Exemple : c. Cas où la valeur f(x0) en x0 n'est pas la "bonne"
Soit \(\displaystyle{f_3 :\mathbb R\to\mathbb R,\textrm{ telle que } f(x)=0\textrm{ pour }x\neq0\textrm{ et } f(0)=1}\)
La fonction \(f_3\) n'est pas continue en \(0\) : elle est bien définie en \(0\) mais la valeur \(1\), qu'elle prend en ce point, ne répond pas à la définition de la continuité; a priori on peut résumer la situation en disant que \(f_3\) n'a pas la "bonne" valeur en \(0\). La valeur \(0\) satisfait à la condition :
\(\displaystyle{\forall\epsilon>0,\exists\eta>0,\forall x\in\mathbb R^*\quad(\vert x\vert<\eta\Rightarrow\vert f_3(x)\vert<\epsilon)}\),
mais pas \(1\) qui est la valeur de \(f_3\) en \(0\).
Deux points de vue sont alors possibles:
ou on "retire" \(0\) et on prolonge la restriction de \(f_3 \textrm{ à }\mathbb R^*\) par continuité, on a alors la fonction nulle
ou on ne "retire" pas \(0\) et alors il n'y a pas de prolongement envisageable.
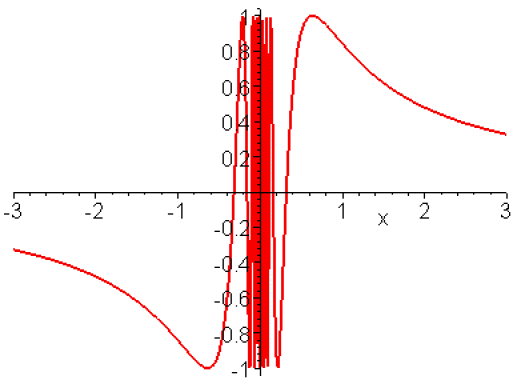
Exemple : d. Cas où il n'y a pas de prolongement possible en x0
Soit \(\displaystyle{f_4 :\mathbb R^*\to\mathbb R\quad x\mapsto\sin\left(\frac{1}{x}\right)}\)
Comme dans l'exemple a. le point \(0\) n'appartient pas à l'ensemble de définition, mais ici la fonction oscille indéfiniment entre \(-1\) et \(+1\), comme on peut le mettre en évidence en considérant la suite \((u_n)\) définie par :
\(\displaystyle{u_{2n}=\frac{1}{n\pi},\quad u_{2n+1}=\frac{2}{(4n+1)\pi}}\)
on a donc \(f_4(u_{2n})=0 \textrm{ et }f_4(u_{2n+1})=1\).
La suite \((u_n)\) a pour limite \(0\) et la suite \((f_4(u_n))\) n'est pas convergente.
La fonction \(f_4\) est bornée au voisinage de \(0\) mais, quelle que soit la valeur qu'on lui attribue en \(0\), la fonction ainsi prolongée n'est pas continue. On formalise ainsi cette situation :
\(\displaystyle{\forall l\in\mathbb R,\exists\epsilon>0,\forall\eta>0,\exists x\in\mathbb R^*\quad(\vert x\vert<\eta\textrm{ et }\vert f_4(x)-l\vert\geq \epsilon)}\) .
On ne peut donc pas prolonger par continuité \(f_4\) en \(0\); on dira que \(f_4\) n'a pas de limite quand \(x\) tend vers \(0\).
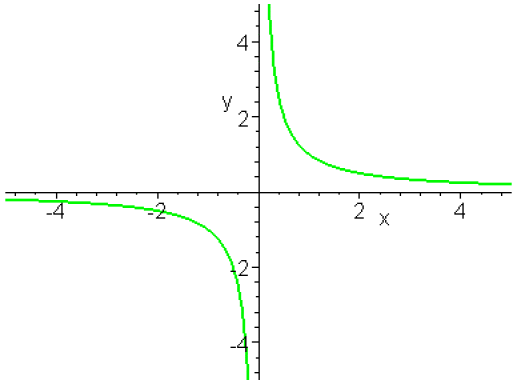
Exemple : e. Cas où la fonction tend vers + l'infini quand la variable tend vers x0
Soit \(\displaystyle{f_5 :\mathbb R_+^*\to\mathbb R\quad x\mapsto\frac{1}{x}}\)
Le point \(0\) n'appartient pas à l'ensemble de définition et il ne peut être question de prolonger \(f_5\) par continuité en \(0\) puisque la fonction n'est pas bornée au voisinage de \(0\).
Quand \(x\) tend vers \(0\) la valeur de \(f_5(x)\) devient "très grande" ce qui signifie :
\(\displaystyle{\forall A,\exists\eta>0,\forall x>0\quad(0< x<\eta\Rightarrow f_5(x)> A)}\)
On dira que la fonction \(f_5\) tend vers \(+\infty\) ou que \(f_5(x)\) est un infiniment grand positif quand \(x\) tend vers \(0\), ce concept sera défini et étudié au paragraphe 2.2.
On peut encore étudier cette fonction quand \(x\) appartient à un voisinage de \(+\infty\): quand \(x\) prend des valeurs très grandes \(f_5(x)\) prend des valeurs voisines de \(0\); on dit que \(f_5(x)\) est un infiniment petit quand \(x\) tend vers \(+\infty\), ce que l'on traduit :
\(\displaystyle{\forall\epsilon>0,\exists B>0,\forall x>0\quad(x> B\Rightarrow0< f_5(x)<\epsilon)}\)
D'où le concept de limite pour \(x\) tendant vers \(+\infty\).
Exemple : f. Étude d'une fonction qui n'est pas continue en une infinité de points
Soit \(f_6\) définie sur \(\mathbb R\) par \(f_6(x)=x\) si \(x\in\mathbb Q\) et \(f_6(x)=\frac{1}{x}\) si \(x\in\mathbb R\setminus \mathbb Q\)
On remarque que \(f_6\) est une bijection de \(\mathbb R\) sur \(\mathbb R\), en effet, pour tout réel \(y\), l'équation \(y= f_6(x)\) admet une solution et une seule :
\(\displaystyle{\begin{array}{lll}y&\in&\mathbb Q\Rightarrow x=y\\y&\in&\mathbb R\setminus \mathbb Q,y\neq0,\Rightarrow x=\frac{1}{y}\end{array}}\)
Nous allons montrer que \(f_6\) est continue en deux points seulement.
Soit \(x_0\in\mathbb R\setminus \mathbb Q: x_0\) est limite d'une suite de rationnels, par exemple la suite \((u_n)\) définie par
\(\displaystyle{u_n=\frac{[10^nx_0]}{10^n}}\)
On a \(f_6(u_n)=u_n\), d'où \(\displaystyle{\lim_{n\to+\infty}f_6(u_n)=x_0\neq f_6(x_0)}\) car l'égalité \(x = f_6(x)\) entraîne \(x\in\mathbb Q\).
La fonction \(f_6\) n'est pas continue en \(x_0\).
Soit \(x_0\in\mathbb Q,x_0\) est limite d'une suite d'irrationnels, par exemple \((v_n)\) définie par
\(\displaystyle{v_n=x_0+\frac{\pi}{n}}\).
On a alors \(\displaystyle{f_6(v_n)=\frac{1}{v_n}}\) d'où si \(\displaystyle{x_0\neq0,\lim_{n\to+\infty}f_6(v_n)=\frac{1}{x_0}\neq x_0=f_6(x_0)}\) sauf si \(x_0=1\) ou \(x_0=-1\).
Le cas \(x_0=0\) se traite de la même façon.
La fonction \(f_6\) n'est pas continue en tout point \(x_0\) rationnel différent de 1 et -1.
On a donc montré que \(f_6\) n'est pas continue en tout point différent de 1 et -1 ; on n'a pas montré qu'elle est effectivement continue en 1 et -1, car on a considéré seulement quelques suites et non toutes les suites qui convergent vers ces points. Pour montrer la continuité en 1 il faut montrer :
\(\displaystyle{\forall\epsilon>0,\exists\eta>0,\forall x\in\mathbb R\quad(\vert x-1\vert<\eta\Rightarrow\vert f_6(x)-1\vert<\epsilon)}\).
Or, la continuité de la fonction \(\displaystyle{x\mapsto\frac{1}{x}}\) au point \(1\) entraîne :
\(\displaystyle{\exists\alpha>0,\forall x\in\mathbb R\quad(\vert x-1\vert<\alpha\Rightarrow\left\vert\frac{1}{x}-1\right\vert<\epsilon)}\).
En prenant \(\displaystyle{\eta=\inf(\alpha,\epsilon)}\) on a :
\(\displaystyle{x\in\mathbb Q :\vert x-1\vert<\eta\Rightarrow\vert x-1\vert<\epsilon,\quad x\in\mathbb R\setminus \mathbb Q\quad\vert x-1\vert<\eta\Rightarrow\left\vert\frac{1}{x}-1\right\vert<\epsilon}\),
d'où finalement \(\displaystyle{\vert f_6(x)-1\vert<\epsilon}\).
La démonstration est analogue pour le point \(-1\). La fonction \(f_6\) est donc continue seulement aux points 1 et -1.